Posts for Tag: graph
Interactive Spirograph
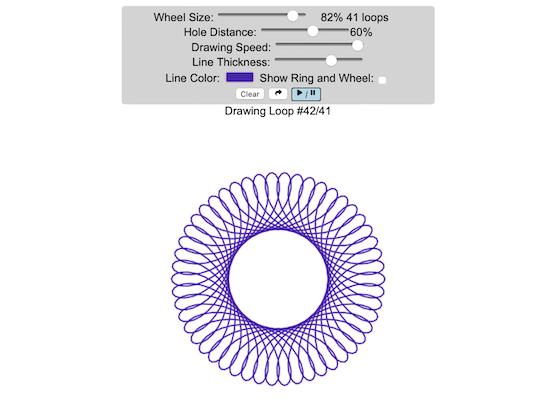
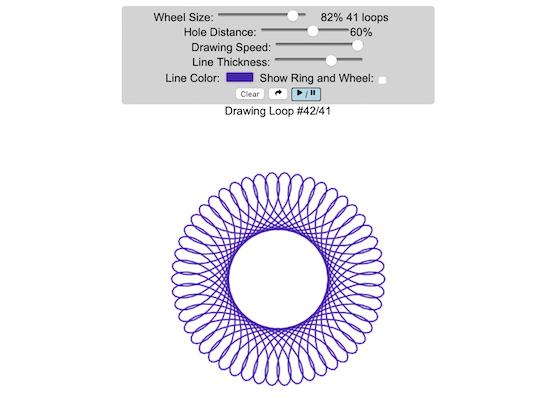
Play with an interactive spirograph and share your creations with your friends. Just play around with the controls at the top and see what interesting designs you can come up with.
Instructions
– Wheel Size controls the size of the wheel inside the ring
– Hole Distance controls the distance from the center of the wheel and the edge
– Drawing Speed controls the speed at which the spirograph is spins
– Line Thickness controls the thickness of the line on the drawing
– Line Color is a color picker letting you change the color of the lines
– Show Ring and Wheel lets you toggle whether the Ring and Wheel are showing
– Clear erases the design
– generates a custom URL and copies it to the clipboard so you can share this exact design with your friends.
– / allows you to start and stop the spirograph animation
Equations
The spirographs shown here are hypotrochoids, which is described as a curve generated by tracing a point attached to a circle that rolls around the interior of a larger circle. The equations for the curve are:
\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}
Sources and Tools
The equations for the spirograph hypotrochoids are from Wikipedia. The drawings and UI are made using canvas and HTML/Javascript and CSS.
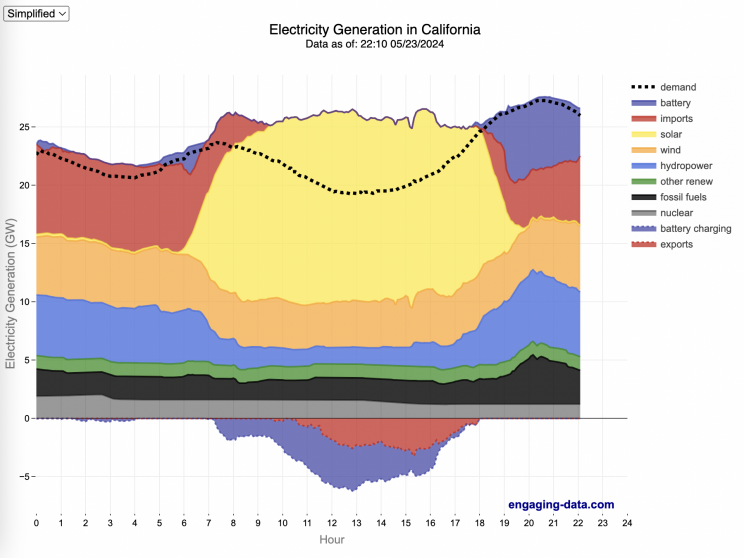
California Electricity Generation
What are the main sources of California’s electricity?
I added the option to view the graph for any day or monthly average from April 2018 to the present using the calendar picker.
In the United States, electric power plant emissions account for about 25% of greenhouse gas emissions. However, California has been a leader in the transition to clean and renewable energy, driven by ambitious climate policies and a commitment to reducing greenhouse gas emissions. The state has set an electricity target for the state of 60% renewables by 2030 and 100% zero-carbon, clean electricity by 2045. To meet these targets, the state has been investing heavily into solar and wind energy sources. Solar is the largest proportion of California’s electricity grid and California now generates more solar energy than any other state.
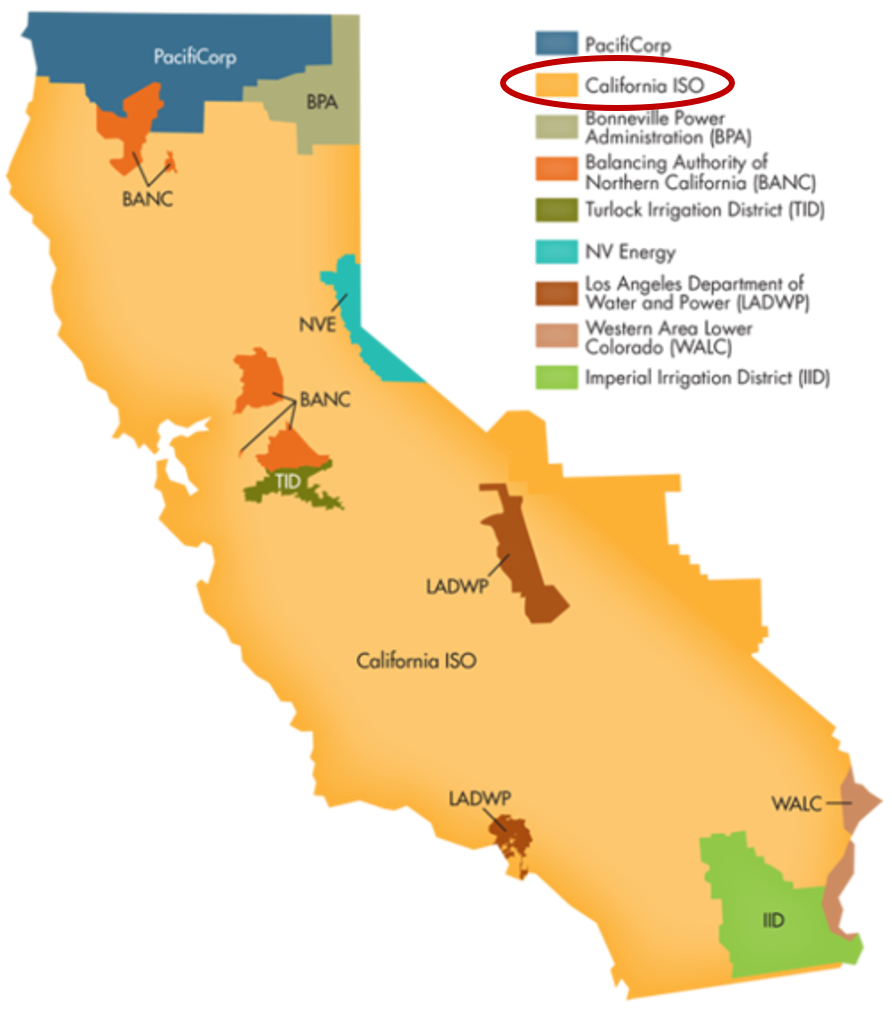
The California Independent System Operator manages the grid for around 32 million Californians or about 80% of the total demand in the state. Here is a map showing the service area and the other electricity districts in the state, the main exceptions include the city of LA and the Sacramento area.
How to read the graph of California’s electricity
The graphs shown here allow us to visualize how electricity generation in the California Independent System Operator (CAISO) region varies over the course of the day. We can see how solar ramps up to be a huge contributor in the middle of the day. And overall, the vast majority of the generation in the state is one form of renewable electricity or another (e.g. solar, wind, hydro, geothermal, biomass and biogas). Add in a small contribution from zero-carbon nuclear energy and we can see that a large majority of power generation comes from zero-carbon sources. It also shows the total electricity demand, which should always be less than the total electricity supply in the state.
Because of the intermittent nature of some renewables, like wind and solar, there are times where the demand for electricity is not able to be met by these sources, and other options are needed to maintain supply demand balance on the state’s grid. To address this issue, the state relies on importing power from outside of the state as well as energy storage (primarily batteries) to meet electricity demand when renewable energy supply is low. If demand is much less than supply, then likely there will be power exported or some charging of batteries. And if demand is less than total generation in the state, power will be imported and/or batteries will be discharged to make up for the power shortfall.
On the graph, positive values from batteries and imports is when those sources are supplying power to the California grid. Negative values for batteries and exports are when there is excess power in the state and batteries are being charged up or power is being exported to neighboring states.
You can view the graph in two forms:
- Detailed – shows all of the power plant fuel types that is provided in the CAISO data: Solar, Wind, Nuclear, Coal, Other, Natural Gas, Large Hydropower, Small Hydropower, Geothermal, Biomass and Biogas. In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
- Simplified – I aggregated the categories from CAISO into Solar, Wind, Nuclear, Fossil Fuel (including Coal, Other and Natural Gas), Hydro (Large and Small Hydropower), and Other Renewable (Geothermal, Biomass and Biogas). In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
Also, I added the ability to see yesterday’s data as well. In the future, I will add the ability to see other dates as well.
Data Sources and Tools
Data for electricity sources for California grid comes from the California Independent System Operator (CAISO). This data from this site is downloaded and processed using a python script and updated every 5 minutes. The graph is made using the open source Plotly javascript graphing library.
NYT Digits Solver
You can play new daily Digits puzzles
Calculate the solution to any digits puzzle
This tool lets you view all of the potential solutions to a Digits puzzle. Enter the goal number and the five starting numbers separated by a comma like “1,2,3,4,5” and hit the “Calculate Solutions” button to see all of the possible solutions to the puzzle. The list is likely quite long so you’ll probably need to scroll through all of the solutions in the list.
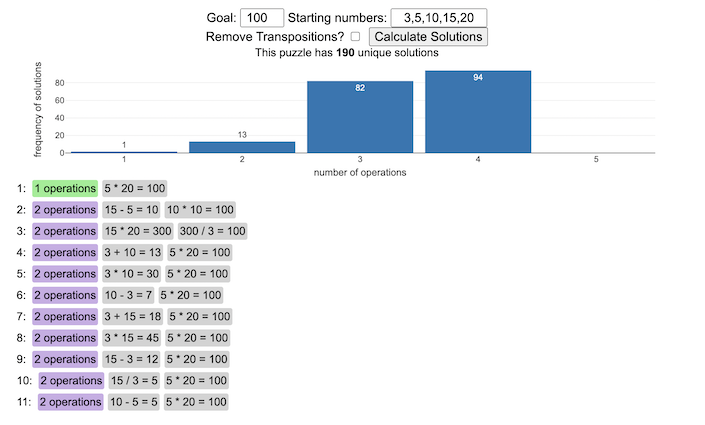
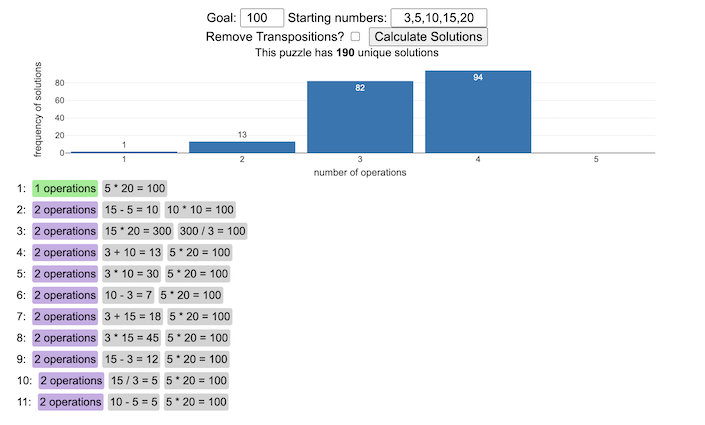
There is also a checkbox that lets you remove transpositions, which are operations that occur in different orders but the same set of operations are used to achieve the final number. For example, where the first two operations appear in reverse order and then are added together in the 3rd operation to hit the target.
e.g. these two solutions are an example of a transposition.
5 + 10 = 15 15 / 3 = 5 5 * 20 = 100
vs
15 / 3 = 5 5 + 10 = 15 5 * 20 = 100
Tools
A version of the solution code is written in Python code and is used to generate the puzzles. This code is re-written in javascript so it is solved inside the browser and the visuals are made with javascript, CSS and HTML and the graphs are made using the open source Plotly javascript graphing library.
Wordle Stats – How Hard is Today’s Wordle?
Update: Just added the ability to look at some previous puzzles (since I started downloading the data from the Wordlebot). Also, you can now view the answers of the puzzles if you click on the eye icon.
What is the distribution of guesses for the daily Wordle?
Wordle is a game of highs and lows. Sometimes your guesses are lucky and you can solve the puzzle easily and sometimes you barely get it in 6 guesses. When the latter happens, sometimes you want validation that that day’s puzzle was hard. This data viz lets you see how other NY Times Wordle players did against the day’s puzzle.
The graph shows the distribution of guesses needed to solve today’s Wordle puzzle, rounded to the nearest whole percent. It also colors the most common number of guesses to solve the puzzle in green and calculates the average number of guesses. “NS” stands for Not Solved.
Even over 1 year later, I still enjoy playing Wordle. I even made a few Wordle games myself – Wordguessr – Tridle – Scrabwordle. I’ve been enjoying the Wordlebot which does a daily analysis of your game. I especially enjoy how it indicates how “lucky” your guesses were and how they eliminated possible answers until you arrive at the puzzle solution. One thing it also provides is data on the frequency of guesses that are made which provides information on the number of guesses it took to solve each puzzle.
I play in the mornings so the graph data will be updated every day at 7am Pacific Time.
Data and Tools
The data comes from playing NY Times Wordle game and using their Wordlebot. Python is used to extract the data and wrangle the data into a clean format. Visualization was done in javascript and specifically the plotly visualization library.
Colorado River Reservoir Levels

How much water is in the main Colorado River reservoirs?
Check out my California Reservoir Levels Dashboard
I based this graph off of my California Reservoir marimekko graph, because many folks were interested in seeing a similar figure for the Colorado river reservoirs.
This is a marimekko (or mekko) graph which may take some time to understand if you aren’t used to seeing them. Each “row” represents one reservoir, with bars showing how much of the reservoir is filled (blue) and unfilled (brown). The height of the “row” indicates how much water the reservoir could hold. Lake Mead is the reservoir with the largest capacity (at almost 29,000 kaf) and so it is the tallest row. The proportion of blue to brown will show how full it is. As with the California version of this graph, there are also lines that represent historical levels, including historical median level for the day of the year (in red) and the 1 year ago level, which is shown as a dark blue line. I also added the “Deadpool” level for the two largest reservoirs. This is the level at which water cannot flow past the dam and is stuck in the reservoir.
Lake Mead and Lake Powell are by far the largest of these reservoirs and also included are several smaller reservoirs (relative to these two) so the bars will be very thin to the point where they are barely a sliver or may not even show up.
Historical Data
Historical data comes from https://www.water-data.com/ and differs for each reservoir.
- Lake Mead – 1941 to 2015
- Lake Powell – 1964 to 2015
- Flaming Gorge – 1972 to 2015
- Lake Mohave – 1952 to 2015
- Lake Navajo – 1969 to 2015
- Blue Mesa – 1969 to 2015
- Lake Havasu – 1939 to 2015
The daily data for each reservoir was captured in this time period and median value for each day of the calendar year was calculated and this is shown as the red line on the graph.
Instructions:
If you are on a computer, you can hover your cursor over a reservoir and the dashboard at the top will provide information about that individual reservoir. If you are on a mobile device you can tap the reservoir to get that same info. It’s not possible to see or really interact with the tiniest slivers. The main goal of this visualization is to provide a quick overview of the status of the main reservoirs along the Colorado River (or that provide water to the Colorado).
Units are in kaf, thousands of acre feet. 1 kaf is the amount of water that would cover 1 acre in one thousand feet of water (or 1000 acres in water in 1 foot of water). It is also the amount of water in a cube that is 352 feet per side (about the length of a football field). Lake Mead is very large and could hold about 35 cubic kilometers of water at full (but not flood) capacity.
Data and Tools
The data on water storage comes from the US Bureau of Reclamation’s Lower Colorado River Water Operations website. Historical reservoir levels comes from the water-data.com website. Python is used to extract the data and wrangle the data in to a clean format, using the Pandas data analysis library. Visualization was done in javascript and specifically the D3.js visualization library.

Visualizing California’s Water Storage – Reservoirs and Snowpack
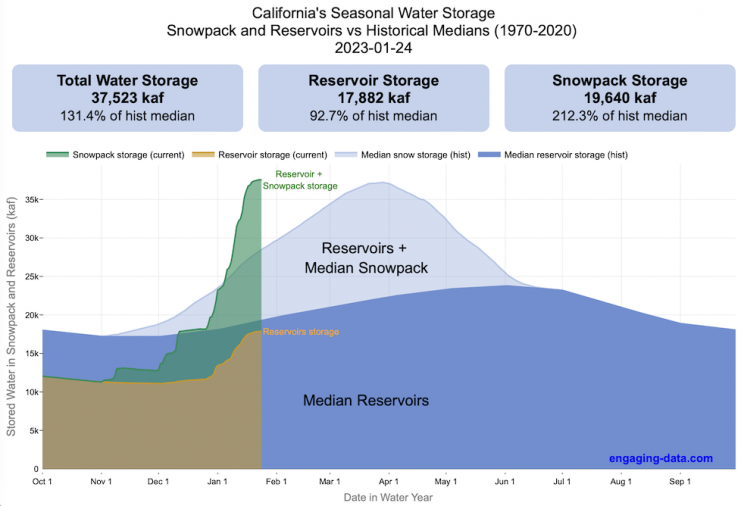
How much water is stored in California’s snowpack and reservoirs?
California’s snow pack is essentially another “reservoir” that is able to store water in the Sierra Nevada mountains. Graphing these things together can give a better picture of the state of California’s water and drought.
The historical median (i.e. 50th percentile) for snow pack water content is stacked on top of the median for reservoirs storage (shown in two shades of blue). The current water year reservoirs is shown in orange and the current year’s snow pack measurement is stacked on top in green. What is interesting is that the typical peak snow pack (around April 1) holds almost as much water (about 2/3 as much) as the reservoirs typically do. However, the reservoirs can store these volumes for much of the year while the snow pack is very seasonal and only does so for a short period of time.
Snowpack is measured at 125 different snow sensor sites throughout the Sierra Nevada mountains. The reservoir value is the total of 50 of the largest reservoirs in California. In both cases, the median is derived from calculating the median values for each day of the year from historical data from these locations from 1970 to 2021.
I’ve been slowly building out the water tracking visualizations tools/dashboards on this site. And with the recent rains (January 2023), there has been quite a bit of interest in these visualizations. One data visualization that I’ve wanted to create is to combine the precipitation and reservoir data into one overarching figure.
Creating the graph
I recently saw one such figure on Twitter by Mike Dettinger, a researcher who studies water/climate issues. The graph shows the current reservoir and snowpack water content overlaid on the historic levels. It is a great graph that conveys quite a bit of info and I thought I would create an interactive version of these while utilizing the automated data processing that’d I’d already created to make my other graphs/dashboards.
Time for another reservoirs-plus-snowpack storage update….LOT of snow up there now and the big Sierra reservoirs (even Shasta!) are already benefitting. Still mostly below average but moving up. Snow stacking up in UCRB. @CW3E_Scripps @DroughtGov https://t.co/2eZgNArahy pic.twitter.com/YEH4IYKlnH
— Mike Dettinger (@mdettinger) January 15, 2023
The challenge was to convert inches of snow water equivalent into a total volume of water in the snowpack, which I asked Mike about. He pointed me to a paper by Margulis et al 2016 that estimates the total volume of water in the Sierra snowpack for 31 years. Since I already had downloaded data on historical snow water equivalents for these same years, I could correlate the estimated peak snow water volume (in cubic km) to the inches of water at these 120 or so Sierra snow sensor sites. I ran a linear regression on these 30 data points. This allowed me to estimate a scaling factor that converts the inches of water equivalent to a volume of liquid water (and convert to thousands of acre feet, which is the same unit as reservoirs are measured in).
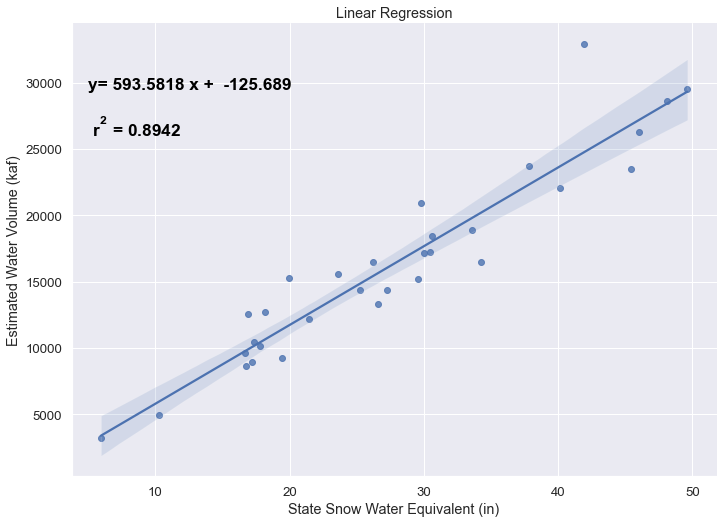
This scaling factor allows me to then graph the snowpack water volume with the reservoir volumes.
See my snowpack visualization/post to see more about snow water equivalents.
My numbers may differ slightly from the numbers reported on the state’s website. The historical percentiles that I calculated are from 1970 until 2020 while I notice the state’s average is between 1990 and 2020.
You can hover (or click) on the graph to audit the data a little more clearly.
Sources and Tools
Data is downloaded from the California Data Exchange Center website of the California Department of Water Resources using a python script. The data is processed in javascript and visualized here using HTML, CSS and javascript and the open source Plotly javascript graphing library.
Interactive Spirograph

Play with an interactive spirograph and share your creations with your friends. Just play around with the controls at the top and see what interesting designs you can come up with.
Instructions
– Wheel Size controls the size of the wheel inside the ring
– Hole Distance controls the distance from the center of the wheel and the edge
– Drawing Speed controls the speed at which the spirograph is spins
– Line Thickness controls the thickness of the line on the drawing
– Line Color is a color picker letting you change the color of the lines
– Show Ring and Wheel lets you toggle whether the Ring and Wheel are showing
– Clear erases the design
– generates a custom URL and copies it to the clipboard so you can share this exact design with your friends.
– / allows you to start and stop the spirograph animation
Equations
The spirographs shown here are hypotrochoids, which is described as a curve generated by tracing a point attached to a circle that rolls around the interior of a larger circle. The equations for the curve are:
\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}
Sources and Tools
The equations for the spirograph hypotrochoids are from Wikipedia. The drawings and UI are made using canvas and HTML/Javascript and CSS.

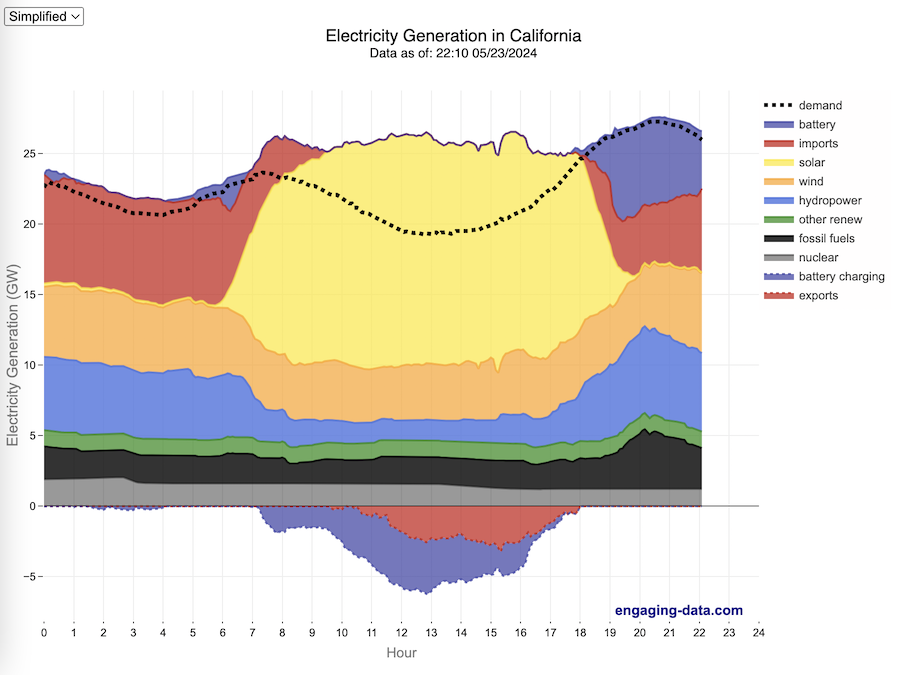
California Electricity Generation

What are the main sources of California’s electricity?
I added the option to view the graph for any day or monthly average from April 2018 to the present using the calendar picker.
In the United States, electric power plant emissions account for about 25% of greenhouse gas emissions. However, California has been a leader in the transition to clean and renewable energy, driven by ambitious climate policies and a commitment to reducing greenhouse gas emissions. The state has set an electricity target for the state of 60% renewables by 2030 and 100% zero-carbon, clean electricity by 2045. To meet these targets, the state has been investing heavily into solar and wind energy sources. Solar is the largest proportion of California’s electricity grid and California now generates more solar energy than any other state.
The California Independent System Operator manages the grid for around 32 million Californians or about 80% of the total demand in the state. Here is a map showing the service area and the other electricity districts in the state, the main exceptions include the city of LA and the Sacramento area.

How to read the graph of California’s electricity
The graphs shown here allow us to visualize how electricity generation in the California Independent System Operator (CAISO) region varies over the course of the day. We can see how solar ramps up to be a huge contributor in the middle of the day. And overall, the vast majority of the generation in the state is one form of renewable electricity or another (e.g. solar, wind, hydro, geothermal, biomass and biogas). Add in a small contribution from zero-carbon nuclear energy and we can see that a large majority of power generation comes from zero-carbon sources. It also shows the total electricity demand, which should always be less than the total electricity supply in the state.
Because of the intermittent nature of some renewables, like wind and solar, there are times where the demand for electricity is not able to be met by these sources, and other options are needed to maintain supply demand balance on the state’s grid. To address this issue, the state relies on importing power from outside of the state as well as energy storage (primarily batteries) to meet electricity demand when renewable energy supply is low. If demand is much less than supply, then likely there will be power exported or some charging of batteries. And if demand is less than total generation in the state, power will be imported and/or batteries will be discharged to make up for the power shortfall.
On the graph, positive values from batteries and imports is when those sources are supplying power to the California grid. Negative values for batteries and exports are when there is excess power in the state and batteries are being charged up or power is being exported to neighboring states.
You can view the graph in two forms:
- Detailed – shows all of the power plant fuel types that is provided in the CAISO data: Solar, Wind, Nuclear, Coal, Other, Natural Gas, Large Hydropower, Small Hydropower, Geothermal, Biomass and Biogas. In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
- Simplified – I aggregated the categories from CAISO into Solar, Wind, Nuclear, Fossil Fuel (including Coal, Other and Natural Gas), Hydro (Large and Small Hydropower), and Other Renewable (Geothermal, Biomass and Biogas). In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
Also, I added the ability to see yesterday’s data as well. In the future, I will add the ability to see other dates as well.
Data Sources and Tools
Data for electricity sources for California grid comes from the California Independent System Operator (CAISO). This data from this site is downloaded and processed using a python script and updated every 5 minutes. The graph is made using the open source Plotly javascript graphing library.

NYT Digits Solver

You can play new daily Digits puzzles
Calculate the solution to any digits puzzle
This tool lets you view all of the potential solutions to a Digits puzzle. Enter the goal number and the five starting numbers separated by a comma like “1,2,3,4,5” and hit the “Calculate Solutions” button to see all of the possible solutions to the puzzle. The list is likely quite long so you’ll probably need to scroll through all of the solutions in the list.
There is also a checkbox that lets you remove transpositions, which are operations that occur in different orders but the same set of operations are used to achieve the final number. For example, where the first two operations appear in reverse order and then are added together in the 3rd operation to hit the target.
e.g. these two solutions are an example of a transposition.
5 + 10 = 15 15 / 3 = 5 5 * 20 = 100
vs
15 / 3 = 5 5 + 10 = 15 5 * 20 = 100
Tools
A version of the solution code is written in Python code and is used to generate the puzzles. This code is re-written in javascript so it is solved inside the browser and the visuals are made with javascript, CSS and HTML and the graphs are made using the open source Plotly javascript graphing library.

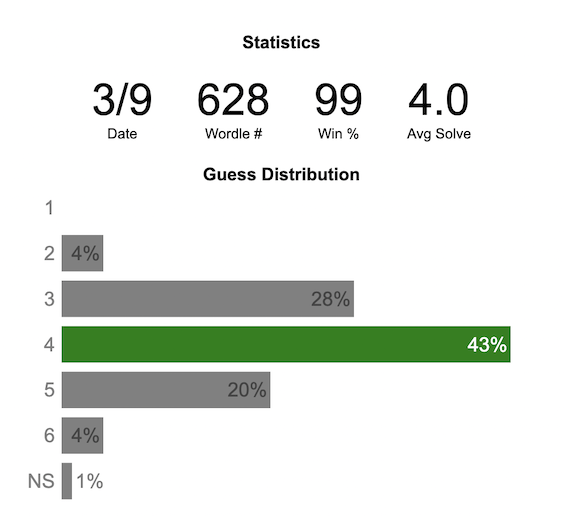
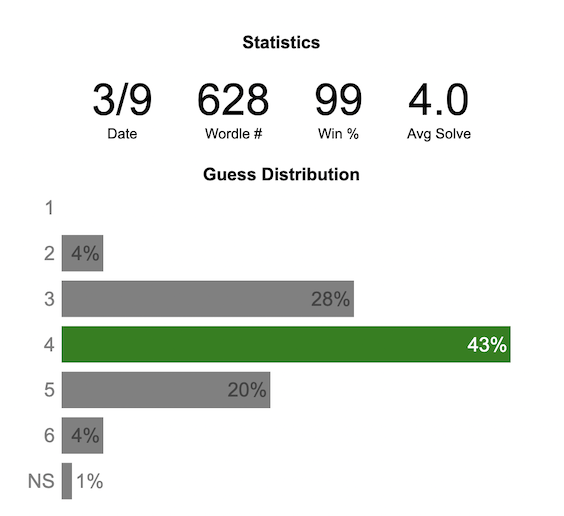
Wordle Stats – How Hard is Today’s Wordle?

Update: Just added the ability to look at some previous puzzles (since I started downloading the data from the Wordlebot). Also, you can now view the answers of the puzzles if you click on the eye icon.
What is the distribution of guesses for the daily Wordle?
Wordle is a game of highs and lows. Sometimes your guesses are lucky and you can solve the puzzle easily and sometimes you barely get it in 6 guesses. When the latter happens, sometimes you want validation that that day’s puzzle was hard. This data viz lets you see how other NY Times Wordle players did against the day’s puzzle.
The graph shows the distribution of guesses needed to solve today’s Wordle puzzle, rounded to the nearest whole percent. It also colors the most common number of guesses to solve the puzzle in green and calculates the average number of guesses. “NS” stands for Not Solved.
Even over 1 year later, I still enjoy playing Wordle. I even made a few Wordle games myself – Wordguessr – Tridle – Scrabwordle. I’ve been enjoying the Wordlebot which does a daily analysis of your game. I especially enjoy how it indicates how “lucky” your guesses were and how they eliminated possible answers until you arrive at the puzzle solution. One thing it also provides is data on the frequency of guesses that are made which provides information on the number of guesses it took to solve each puzzle.
I play in the mornings so the graph data will be updated every day at 7am Pacific Time.
Data and Tools
The data comes from playing NY Times Wordle game and using their Wordlebot. Python is used to extract the data and wrangle the data into a clean format. Visualization was done in javascript and specifically the plotly visualization library.

Colorado River Reservoir Levels

How much water is in the main Colorado River reservoirs?
Check out my California Reservoir Levels Dashboard
I based this graph off of my California Reservoir marimekko graph, because many folks were interested in seeing a similar figure for the Colorado river reservoirs.
This is a marimekko (or mekko) graph which may take some time to understand if you aren’t used to seeing them. Each “row” represents one reservoir, with bars showing how much of the reservoir is filled (blue) and unfilled (brown). The height of the “row” indicates how much water the reservoir could hold. Lake Mead is the reservoir with the largest capacity (at almost 29,000 kaf) and so it is the tallest row. The proportion of blue to brown will show how full it is. As with the California version of this graph, there are also lines that represent historical levels, including historical median level for the day of the year (in red) and the 1 year ago level, which is shown as a dark blue line. I also added the “Deadpool” level for the two largest reservoirs. This is the level at which water cannot flow past the dam and is stuck in the reservoir.
Lake Mead and Lake Powell are by far the largest of these reservoirs and also included are several smaller reservoirs (relative to these two) so the bars will be very thin to the point where they are barely a sliver or may not even show up.
Historical Data
Historical data comes from https://www.water-data.com/ and differs for each reservoir.
- Lake Mead – 1941 to 2015
- Lake Powell – 1964 to 2015
- Flaming Gorge – 1972 to 2015
- Lake Mohave – 1952 to 2015
- Lake Navajo – 1969 to 2015
- Blue Mesa – 1969 to 2015
- Lake Havasu – 1939 to 2015
The daily data for each reservoir was captured in this time period and median value for each day of the calendar year was calculated and this is shown as the red line on the graph.
Instructions:
If you are on a computer, you can hover your cursor over a reservoir and the dashboard at the top will provide information about that individual reservoir. If you are on a mobile device you can tap the reservoir to get that same info. It’s not possible to see or really interact with the tiniest slivers. The main goal of this visualization is to provide a quick overview of the status of the main reservoirs along the Colorado River (or that provide water to the Colorado).
Units are in kaf, thousands of acre feet. 1 kaf is the amount of water that would cover 1 acre in one thousand feet of water (or 1000 acres in water in 1 foot of water). It is also the amount of water in a cube that is 352 feet per side (about the length of a football field). Lake Mead is very large and could hold about 35 cubic kilometers of water at full (but not flood) capacity.
Data and Tools
The data on water storage comes from the US Bureau of Reclamation’s Lower Colorado River Water Operations website. Historical reservoir levels comes from the water-data.com website. Python is used to extract the data and wrangle the data in to a clean format, using the Pandas data analysis library. Visualization was done in javascript and specifically the D3.js visualization library.

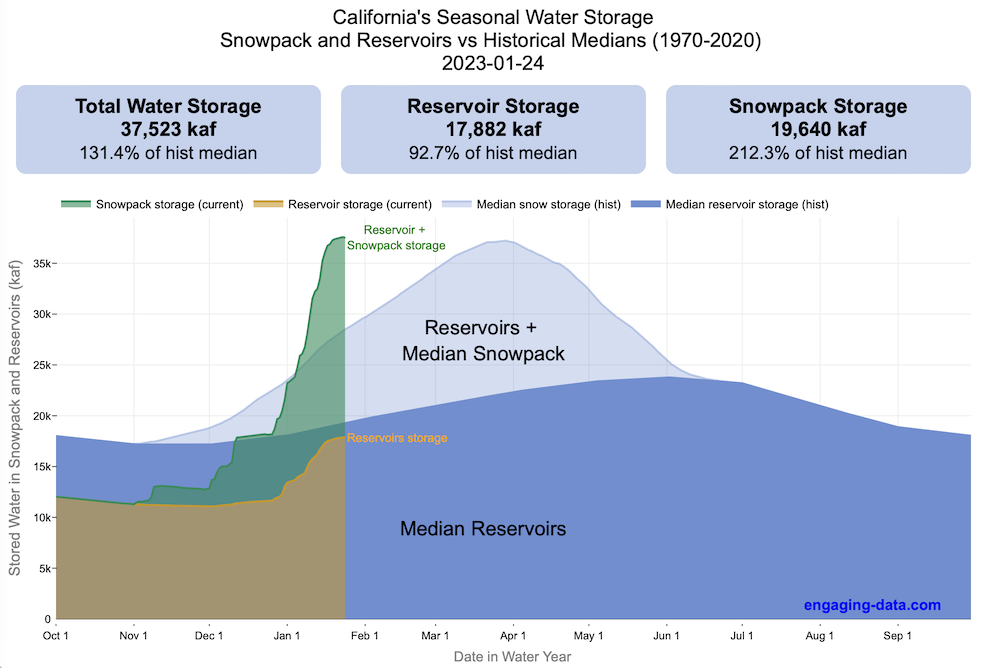
Visualizing California’s Water Storage – Reservoirs and Snowpack

How much water is stored in California’s snowpack and reservoirs?
California’s snow pack is essentially another “reservoir” that is able to store water in the Sierra Nevada mountains. Graphing these things together can give a better picture of the state of California’s water and drought.
The historical median (i.e. 50th percentile) for snow pack water content is stacked on top of the median for reservoirs storage (shown in two shades of blue). The current water year reservoirs is shown in orange and the current year’s snow pack measurement is stacked on top in green. What is interesting is that the typical peak snow pack (around April 1) holds almost as much water (about 2/3 as much) as the reservoirs typically do. However, the reservoirs can store these volumes for much of the year while the snow pack is very seasonal and only does so for a short period of time.
Snowpack is measured at 125 different snow sensor sites throughout the Sierra Nevada mountains. The reservoir value is the total of 50 of the largest reservoirs in California. In both cases, the median is derived from calculating the median values for each day of the year from historical data from these locations from 1970 to 2021.
I’ve been slowly building out the water tracking visualizations tools/dashboards on this site. And with the recent rains (January 2023), there has been quite a bit of interest in these visualizations. One data visualization that I’ve wanted to create is to combine the precipitation and reservoir data into one overarching figure.
Creating the graph
I recently saw one such figure on Twitter by Mike Dettinger, a researcher who studies water/climate issues. The graph shows the current reservoir and snowpack water content overlaid on the historic levels. It is a great graph that conveys quite a bit of info and I thought I would create an interactive version of these while utilizing the automated data processing that’d I’d already created to make my other graphs/dashboards.
Time for another reservoirs-plus-snowpack storage update….LOT of snow up there now and the big Sierra reservoirs (even Shasta!) are already benefitting. Still mostly below average but moving up. Snow stacking up in UCRB. @CW3E_Scripps @DroughtGov https://t.co/2eZgNArahy pic.twitter.com/YEH4IYKlnH
— Mike Dettinger (@mdettinger) January 15, 2023
The challenge was to convert inches of snow water equivalent into a total volume of water in the snowpack, which I asked Mike about. He pointed me to a paper by Margulis et al 2016 that estimates the total volume of water in the Sierra snowpack for 31 years. Since I already had downloaded data on historical snow water equivalents for these same years, I could correlate the estimated peak snow water volume (in cubic km) to the inches of water at these 120 or so Sierra snow sensor sites. I ran a linear regression on these 30 data points. This allowed me to estimate a scaling factor that converts the inches of water equivalent to a volume of liquid water (and convert to thousands of acre feet, which is the same unit as reservoirs are measured in).

This scaling factor allows me to then graph the snowpack water volume with the reservoir volumes.
See my snowpack visualization/post to see more about snow water equivalents.
My numbers may differ slightly from the numbers reported on the state’s website. The historical percentiles that I calculated are from 1970 until 2020 while I notice the state’s average is between 1990 and 2020.
You can hover (or click) on the graph to audit the data a little more clearly.
Sources and Tools
Data is downloaded from the California Data Exchange Center website of the California Department of Water Resources using a python script. The data is processed in javascript and visualized here using HTML, CSS and javascript and the open source Plotly javascript graphing library.

Recent Comments