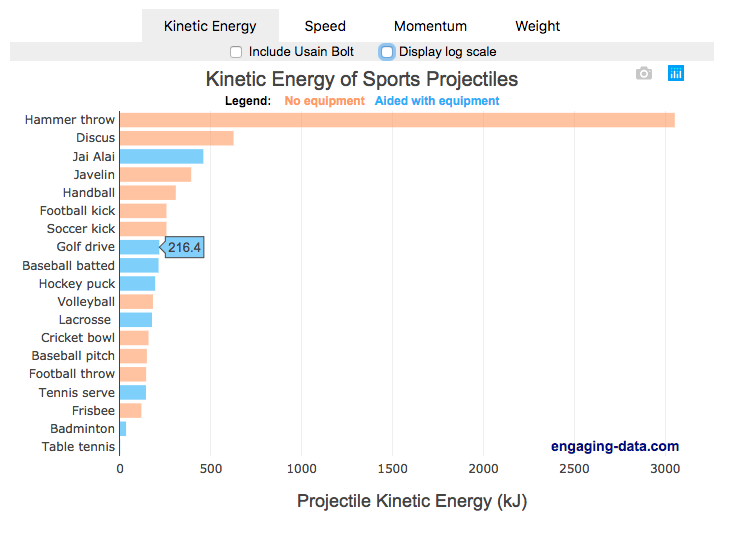
I’ve been playing (and watching) alot of soccer recently with the kids and it got me thinking about how hard the pros can kick the ball compared to us. This got me thinking about how much energy athletes can impart to a soccer ball and how that compares to balls and projectiles in other sports. This is not a scientific study, as I just googled the fastest pitch, shot, serve, kick, throw etc. from a variety of sports and the weight of the respective balls/projectiles to calculate their kinetic energy and momentum. I added in the stats for a (sort of) human projectile for comparison as well (Usain Bolt).
The graph is color coded so orange refers to projectiles that require no additional equipment, while the blue requires a bat or racket or club to aid in hitting the ball. You can toggle between log and linear scale on the x-axis to better see the differences between different projectiles.
The hammer throw is interesting because it far exceeds the kinetic energy and momentum of the other balls. If you watch a video of olympic hammer throws, you’ll see how much energy these very large, strong athletes are able to put into the throw. I think another aspect is that the top kinetic energy projectiles are all throws where there is significant acceleration of the projectile over a longer period of time rather than an instantaneous kick or hit.
Switching to the speed tab, all of the fastest projectiles are aided by equipment to achieve their very high speeds, but generally these projectiles have lower weights. This is also seen in the momentum tab, where the heavier projectiles are mostly unaided by equipment, probably because of the challenge of imparting enough momentum onto a heavy ball/projectile would require accelerating an even heavier racket/bat.
Equations and stuff
The equation for kinetic energy is \(E = {1\over2} mv^2\),
where E is kinetic energy (expressed in joules or kilojoules), m is mass and v is velocity (or speed).
The equation for momentum is \(P = mv\), where P is momentum.
The difference between momentum and kinetic energy is slightly tricky. The momentum rankings seem to prioritize the mass of the projectile while kinetic energy is a balance between speed (velocity) and mass. In kicking, throwing or hitting a ball/projectile, the player needs to put impart the energy into the ball. In a collision, total momentum of the system (player and ball) is conserved but kinetic energy is not, although total energy is (some energy may be “lost” as heat, sound, etc). In terms of being “hit” by the projectile, I believe that kinetic energy is probably more important than momentum for gauging the overall effect of the impact, but the total energy is not the only concern.The area over which the impact would occur is also important. Honestly, the table tennis (ping-pong) ball is the only one I think I’d be okay getting hit by (at least at these world record speeds).
Data sources and tools:
Mostly google for ball weights and trying to find some mention of the “fastest” throw or kick or whatever. Calculations are made using the equations above and plotted using Plot.ly javascript library.
Related Posts
1 Comment »


One Response to Speed and Kinetic Energy of Sports Pitches, Shots and Kicks
Very interesting comparison! However I think you’re you’re using kJ where it should be Joules. For comparison, a 2000 kg vehicle travelling at 100 km/h (about 60 mph, or 27.78 m/s) has KE of 0.5 x (2000 x 27.78 x 27.78) =771,605J. = 771.6 kJ. Five baseball-pitches will not hit like a 2-tonne car doing 60 mph, however legendary the pitcher!