Posts for Tag: visualization
Interactive Spirograph
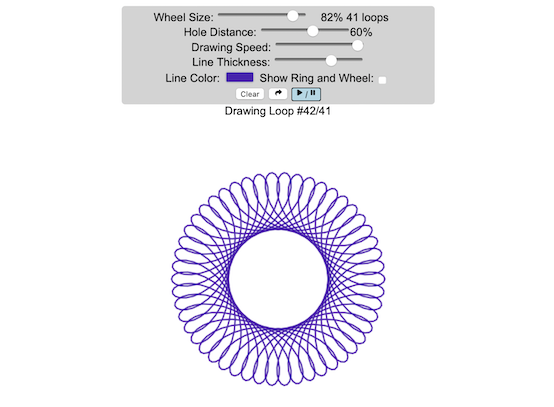
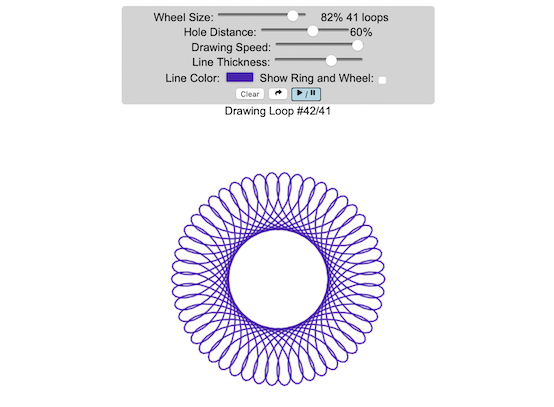
Play with an interactive spirograph and share your creations with your friends. Just play around with the controls at the top and see what interesting designs you can come up with.
Instructions
– Wheel Size controls the size of the wheel inside the ring
– Hole Distance controls the distance from the center of the wheel and the edge
– Drawing Speed controls the speed at which the spirograph is spins
– Line Thickness controls the thickness of the line on the drawing
– Line Color is a color picker letting you change the color of the lines
– Show Ring and Wheel lets you toggle whether the Ring and Wheel are showing
– Clear erases the design
– generates a custom URL and copies it to the clipboard so you can share this exact design with your friends.
– / allows you to start and stop the spirograph animation
Equations
The spirographs shown here are hypotrochoids, which is described as a curve generated by tracing a point attached to a circle that rolls around the interior of a larger circle. The equations for the curve are:
\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}
Sources and Tools
The equations for the spirograph hypotrochoids are from Wikipedia. The drawings and UI are made using canvas and HTML/Javascript and CSS.
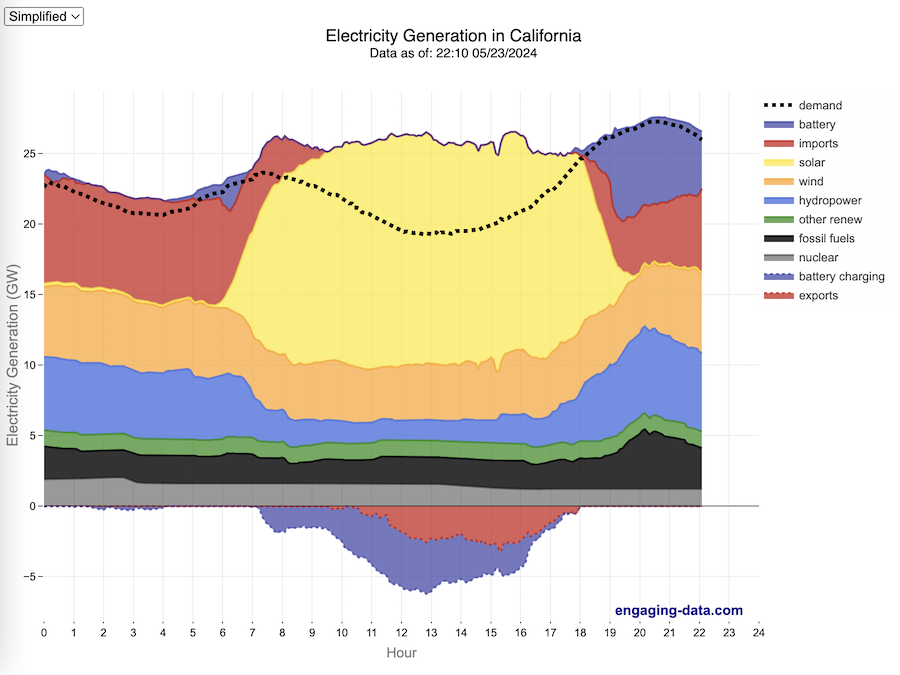
California Electricity Generation
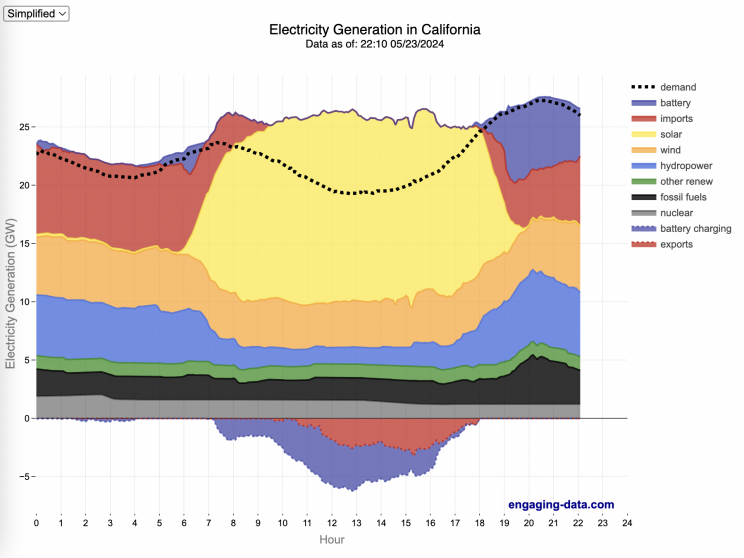
What are the main sources of California’s electricity?
I added the option to view the graph for any day or monthly average from April 2018 to the present using the calendar picker.
In the United States, electric power plant emissions account for about 25% of greenhouse gas emissions. However, California has been a leader in the transition to clean and renewable energy, driven by ambitious climate policies and a commitment to reducing greenhouse gas emissions. The state has set an electricity target for the state of 60% renewables by 2030 and 100% zero-carbon, clean electricity by 2045. To meet these targets, the state has been investing heavily into solar and wind energy sources. Solar is the largest proportion of California’s electricity grid and California now generates more solar energy than any other state.
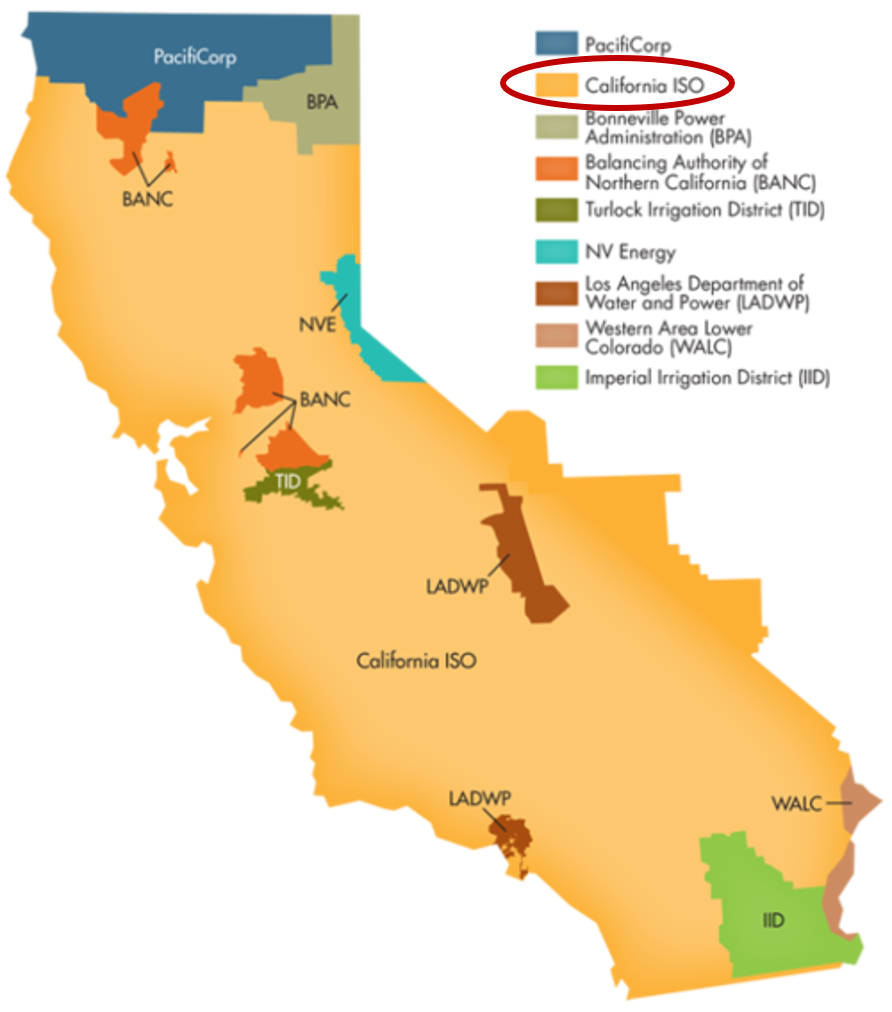
The California Independent System Operator manages the grid for around 32 million Californians or about 80% of the total demand in the state. Here is a map showing the service area and the other electricity districts in the state, the main exceptions include the city of LA and the Sacramento area.
How to read the graph of California’s electricity
The graphs shown here allow us to visualize how electricity generation in the California Independent System Operator (CAISO) region varies over the course of the day. We can see how solar ramps up to be a huge contributor in the middle of the day. And overall, the vast majority of the generation in the state is one form of renewable electricity or another (e.g. solar, wind, hydro, geothermal, biomass and biogas). Add in a small contribution from zero-carbon nuclear energy and we can see that a large majority of power generation comes from zero-carbon sources. It also shows the total electricity demand, which should always be less than the total electricity supply in the state.
Because of the intermittent nature of some renewables, like wind and solar, there are times where the demand for electricity is not able to be met by these sources, and other options are needed to maintain supply demand balance on the state’s grid. To address this issue, the state relies on importing power from outside of the state as well as energy storage (primarily batteries) to meet electricity demand when renewable energy supply is low. If demand is much less than supply, then likely there will be power exported or some charging of batteries. And if demand is less than total generation in the state, power will be imported and/or batteries will be discharged to make up for the power shortfall.
On the graph, positive values from batteries and imports is when those sources are supplying power to the California grid. Negative values for batteries and exports are when there is excess power in the state and batteries are being charged up or power is being exported to neighboring states.
You can view the graph in two forms:
- Detailed – shows all of the power plant fuel types that is provided in the CAISO data: Solar, Wind, Nuclear, Coal, Other, Natural Gas, Large Hydropower, Small Hydropower, Geothermal, Biomass and Biogas. In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
- Simplified – I aggregated the categories from CAISO into Solar, Wind, Nuclear, Fossil Fuel (including Coal, Other and Natural Gas), Hydro (Large and Small Hydropower), and Other Renewable (Geothermal, Biomass and Biogas). In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
Also, I added the ability to see yesterday’s data as well. In the future, I will add the ability to see other dates as well.
Data Sources and Tools
Data for electricity sources for California grid comes from the California Independent System Operator (CAISO). This data from this site is downloaded and processed using a python script and updated every 5 minutes. The graph is made using the open source Plotly javascript graphing library.
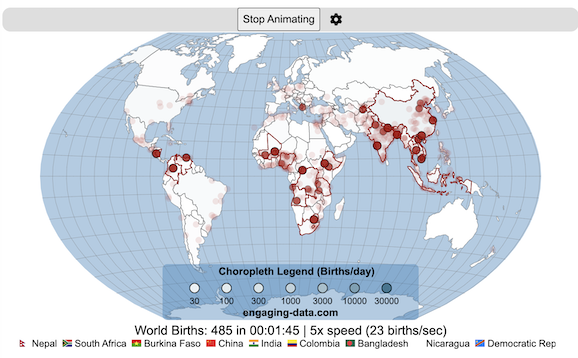
Global Birth Map
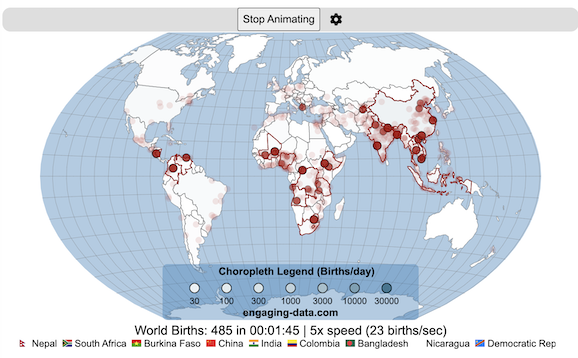
Where in the world are babies being born and how fast?
This interactive, animated map shows the where births are happening across the globe. It doesn’t actually show births in real-time, because data isn’t actually available to do that. However, the map does show the frequency of births that are occurring in different locations across the world. And you can see it in two ways, by country and also geo-referenced to specific locations (along a 1degree grid across the globe). There are many different ways to view this global birth map and these options are laid out in the controls at the top of the map. The scrolling list across the bottom also shows the country of each of the dots on the map.
Instructions
- Speed – change the slider to change the rate at which births show up on the map from real-speed to 25x faster
- Map projection – change the map projection
- Highlight country – an outline around the country when a birth occurs
- Choropleth – Build – as each birth occurs, the background color of the country will slowly change to reflect the number of births in the country
- Choropleth – Show – this option colors all the countries to show the number of births per day that occur in the country
- Dots – Show – this is the main feature that shows where each birth is occurring at the frequency that it does occur.
- Dots – Persist – this feature shows where previous births have occurred and the dots get darker as more births happen in that location.
If you hover (or click on mobile) on a country during the animation, it will display how many births have occurred since the animation stared.
Population distribution data combined with country birthrates
I used data that divided and aggregated the world’s population into 1 degree grid spacing across the globe and I assigned the center of each of these grid locations to a country. Then the country’s annual births (i.e. the country’s population times its birthrate) were distributed across all of the populated locations in each country, weighted by the population distribution (i.e. more populated areas got a greater fraction of the births).
Data Sources and Tools
Population and birthrate data for 2023 was obtained from Wikipedia (Population and birth rates). Population distribution across the globe was obtained from Socioeconomic Data and Applications Center (sedac) at Columbia University.
I used python to process country, population distribution data and parse the data into the probability of a birth at each 1 degree x 1 degree location. Then I used javascript to make random draws and predict the number of births for each map location. D3.js was used to create the map elements and html, css and javascript were used to create the user interface.
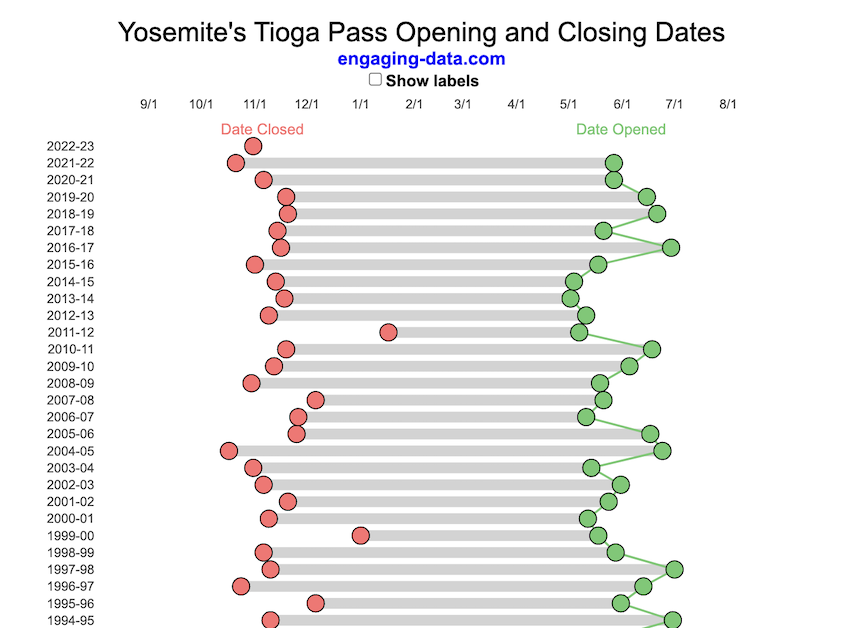
Tioga Pass (Yosemite) Opening Dates
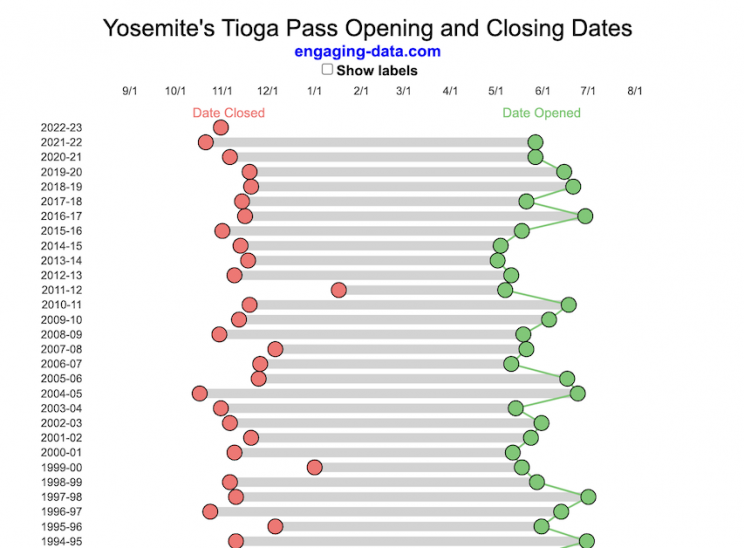
When does Tioga Pass in Yosemite typically open?
The graph shows the closing and opening dates of Tioga pass in Yosemite National Park for each winter season from 1933 to the present. Tioga pass is a mountain pass on State Highway 120 in California’s Sierra Nevada mountain range and one of the entrances to Yosemite NP. The pass itself peaks at 9945 ft above sea level. Each winter it gets a ton of snow, but also with a great deal of variability, which really affects when it can be plowed and the road reopened.
Our family likes to go to Yosemite in June after the kids school lets out and sometimes Hwy 120 and Tioga Pass can often be closed at this time, which limits which areas of the park you can visit. So I often look at data on when the road has opened before and thought it would be a good thing to visualize.
You can toggle the labels on the graph that show the dates of opening and closing as well as the number of days that the pass was closed each winter. Hovering (or clicking) on the circles on the graph will give you a pop up which gives you the exact date.
Data and Tools
The data comes from the US National Park Service for most recent data as well as Mono Basin Clearinghouse for earlier data going back to 1933. Data was organized and compiled in MS Excel. Visualization was done in javascript and specifically the plotly visualization library.
Wordle Stats – How Hard is Today’s Wordle?
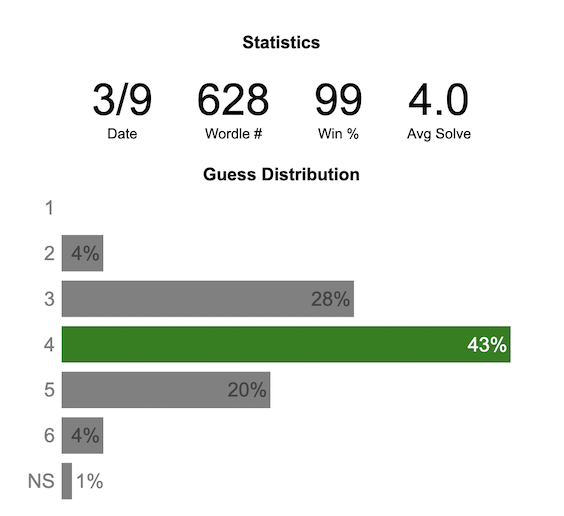
Update: Just added the ability to look at some previous puzzles (since I started downloading the data from the Wordlebot). Also, you can now view the answers of the puzzles if you click on the eye icon.
What is the distribution of guesses for the daily Wordle?
Wordle is a game of highs and lows. Sometimes your guesses are lucky and you can solve the puzzle easily and sometimes you barely get it in 6 guesses. When the latter happens, sometimes you want validation that that day’s puzzle was hard. This data viz lets you see how other NY Times Wordle players did against the day’s puzzle.
The graph shows the distribution of guesses needed to solve today’s Wordle puzzle, rounded to the nearest whole percent. It also colors the most common number of guesses to solve the puzzle in green and calculates the average number of guesses. “NS” stands for Not Solved.
Even over 1 year later, I still enjoy playing Wordle. I even made a few Wordle games myself – Wordguessr – Tridle – Scrabwordle. I’ve been enjoying the Wordlebot which does a daily analysis of your game. I especially enjoy how it indicates how “lucky” your guesses were and how they eliminated possible answers until you arrive at the puzzle solution. One thing it also provides is data on the frequency of guesses that are made which provides information on the number of guesses it took to solve each puzzle.
I play in the mornings so the graph data will be updated every day at 7am Pacific Time.
Data and Tools
The data comes from playing NY Times Wordle game and using their Wordlebot. Python is used to extract the data and wrangle the data into a clean format. Visualization was done in javascript and specifically the plotly visualization library.
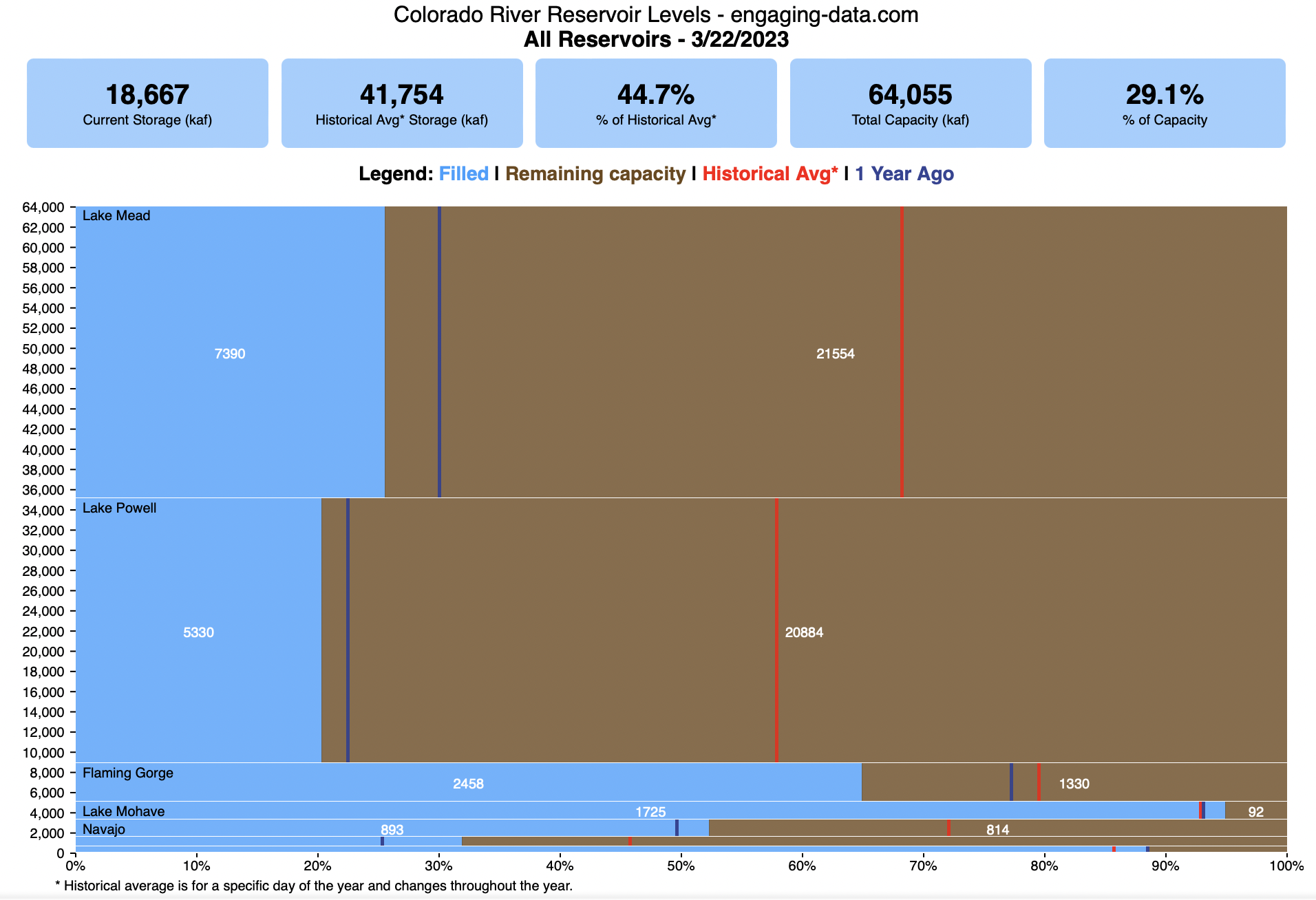
Colorado River Reservoir Levels
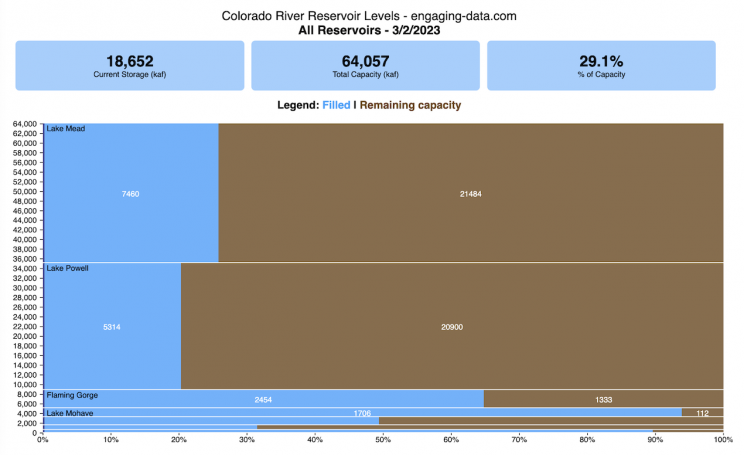
How much water is in the main Colorado River reservoirs?
Check out my California Reservoir Levels Dashboard
I based this graph off of my California Reservoir marimekko graph, because many folks were interested in seeing a similar figure for the Colorado river reservoirs.
This is a marimekko (or mekko) graph which may take some time to understand if you aren’t used to seeing them. Each “row” represents one reservoir, with bars showing how much of the reservoir is filled (blue) and unfilled (brown). The height of the “row” indicates how much water the reservoir could hold. Lake Mead is the reservoir with the largest capacity (at almost 29,000 kaf) and so it is the tallest row. The proportion of blue to brown will show how full it is. As with the California version of this graph, there are also lines that represent historical levels, including historical median level for the day of the year (in red) and the 1 year ago level, which is shown as a dark blue line. I also added the “Deadpool” level for the two largest reservoirs. This is the level at which water cannot flow past the dam and is stuck in the reservoir.
Lake Mead and Lake Powell are by far the largest of these reservoirs and also included are several smaller reservoirs (relative to these two) so the bars will be very thin to the point where they are barely a sliver or may not even show up.
Historical Data
Historical data comes from https://www.water-data.com/ and differs for each reservoir.
- Lake Mead – 1941 to 2015
- Lake Powell – 1964 to 2015
- Flaming Gorge – 1972 to 2015
- Lake Mohave – 1952 to 2015
- Lake Navajo – 1969 to 2015
- Blue Mesa – 1969 to 2015
- Lake Havasu – 1939 to 2015
The daily data for each reservoir was captured in this time period and median value for each day of the calendar year was calculated and this is shown as the red line on the graph.
Instructions:
If you are on a computer, you can hover your cursor over a reservoir and the dashboard at the top will provide information about that individual reservoir. If you are on a mobile device you can tap the reservoir to get that same info. It’s not possible to see or really interact with the tiniest slivers. The main goal of this visualization is to provide a quick overview of the status of the main reservoirs along the Colorado River (or that provide water to the Colorado).
Units are in kaf, thousands of acre feet. 1 kaf is the amount of water that would cover 1 acre in one thousand feet of water (or 1000 acres in water in 1 foot of water). It is also the amount of water in a cube that is 352 feet per side (about the length of a football field). Lake Mead is very large and could hold about 35 cubic kilometers of water at full (but not flood) capacity.
Data and Tools
The data on water storage comes from the US Bureau of Reclamation’s Lower Colorado River Water Operations website. Historical reservoir levels comes from the water-data.com website. Python is used to extract the data and wrangle the data in to a clean format, using the Pandas data analysis library. Visualization was done in javascript and specifically the D3.js visualization library.
Interactive Spirograph

Play with an interactive spirograph and share your creations with your friends. Just play around with the controls at the top and see what interesting designs you can come up with.
Instructions
– Wheel Size controls the size of the wheel inside the ring
– Hole Distance controls the distance from the center of the wheel and the edge
– Drawing Speed controls the speed at which the spirograph is spins
– Line Thickness controls the thickness of the line on the drawing
– Line Color is a color picker letting you change the color of the lines
– Show Ring and Wheel lets you toggle whether the Ring and Wheel are showing
– Clear erases the design
– generates a custom URL and copies it to the clipboard so you can share this exact design with your friends.
– / allows you to start and stop the spirograph animation
Equations
The spirographs shown here are hypotrochoids, which is described as a curve generated by tracing a point attached to a circle that rolls around the interior of a larger circle. The equations for the curve are:
\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}
Sources and Tools
The equations for the spirograph hypotrochoids are from Wikipedia. The drawings and UI are made using canvas and HTML/Javascript and CSS.

California Electricity Generation

What are the main sources of California’s electricity?
I added the option to view the graph for any day or monthly average from April 2018 to the present using the calendar picker.
In the United States, electric power plant emissions account for about 25% of greenhouse gas emissions. However, California has been a leader in the transition to clean and renewable energy, driven by ambitious climate policies and a commitment to reducing greenhouse gas emissions. The state has set an electricity target for the state of 60% renewables by 2030 and 100% zero-carbon, clean electricity by 2045. To meet these targets, the state has been investing heavily into solar and wind energy sources. Solar is the largest proportion of California’s electricity grid and California now generates more solar energy than any other state.
The California Independent System Operator manages the grid for around 32 million Californians or about 80% of the total demand in the state. Here is a map showing the service area and the other electricity districts in the state, the main exceptions include the city of LA and the Sacramento area.

How to read the graph of California’s electricity
The graphs shown here allow us to visualize how electricity generation in the California Independent System Operator (CAISO) region varies over the course of the day. We can see how solar ramps up to be a huge contributor in the middle of the day. And overall, the vast majority of the generation in the state is one form of renewable electricity or another (e.g. solar, wind, hydro, geothermal, biomass and biogas). Add in a small contribution from zero-carbon nuclear energy and we can see that a large majority of power generation comes from zero-carbon sources. It also shows the total electricity demand, which should always be less than the total electricity supply in the state.
Because of the intermittent nature of some renewables, like wind and solar, there are times where the demand for electricity is not able to be met by these sources, and other options are needed to maintain supply demand balance on the state’s grid. To address this issue, the state relies on importing power from outside of the state as well as energy storage (primarily batteries) to meet electricity demand when renewable energy supply is low. If demand is much less than supply, then likely there will be power exported or some charging of batteries. And if demand is less than total generation in the state, power will be imported and/or batteries will be discharged to make up for the power shortfall.
On the graph, positive values from batteries and imports is when those sources are supplying power to the California grid. Negative values for batteries and exports are when there is excess power in the state and batteries are being charged up or power is being exported to neighboring states.
You can view the graph in two forms:
- Detailed – shows all of the power plant fuel types that is provided in the CAISO data: Solar, Wind, Nuclear, Coal, Other, Natural Gas, Large Hydropower, Small Hydropower, Geothermal, Biomass and Biogas. In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
- Simplified – I aggregated the categories from CAISO into Solar, Wind, Nuclear, Fossil Fuel (including Coal, Other and Natural Gas), Hydro (Large and Small Hydropower), and Other Renewable (Geothermal, Biomass and Biogas). In addition, it shows aggregated net imports into the state from other regions as well as battery discharging or charging.
Also, I added the ability to see yesterday’s data as well. In the future, I will add the ability to see other dates as well.
Data Sources and Tools
Data for electricity sources for California grid comes from the California Independent System Operator (CAISO). This data from this site is downloaded and processed using a python script and updated every 5 minutes. The graph is made using the open source Plotly javascript graphing library.

Global Birth Map

Where in the world are babies being born and how fast?
This interactive, animated map shows the where births are happening across the globe. It doesn’t actually show births in real-time, because data isn’t actually available to do that. However, the map does show the frequency of births that are occurring in different locations across the world. And you can see it in two ways, by country and also geo-referenced to specific locations (along a 1degree grid across the globe). There are many different ways to view this global birth map and these options are laid out in the controls at the top of the map. The scrolling list across the bottom also shows the country of each of the dots on the map.
Instructions
- Speed – change the slider to change the rate at which births show up on the map from real-speed to 25x faster
- Map projection – change the map projection
- Highlight country – an outline around the country when a birth occurs
- Choropleth – Build – as each birth occurs, the background color of the country will slowly change to reflect the number of births in the country
- Choropleth – Show – this option colors all the countries to show the number of births per day that occur in the country
- Dots – Show – this is the main feature that shows where each birth is occurring at the frequency that it does occur.
- Dots – Persist – this feature shows where previous births have occurred and the dots get darker as more births happen in that location.
If you hover (or click on mobile) on a country during the animation, it will display how many births have occurred since the animation stared.
Population distribution data combined with country birthrates
I used data that divided and aggregated the world’s population into 1 degree grid spacing across the globe and I assigned the center of each of these grid locations to a country. Then the country’s annual births (i.e. the country’s population times its birthrate) were distributed across all of the populated locations in each country, weighted by the population distribution (i.e. more populated areas got a greater fraction of the births).
Data Sources and Tools
Population and birthrate data for 2023 was obtained from Wikipedia (Population and birth rates). Population distribution across the globe was obtained from Socioeconomic Data and Applications Center (sedac) at Columbia University.
I used python to process country, population distribution data and parse the data into the probability of a birth at each 1 degree x 1 degree location. Then I used javascript to make random draws and predict the number of births for each map location. D3.js was used to create the map elements and html, css and javascript were used to create the user interface.

Tioga Pass (Yosemite) Opening Dates

When does Tioga Pass in Yosemite typically open?
The graph shows the closing and opening dates of Tioga pass in Yosemite National Park for each winter season from 1933 to the present. Tioga pass is a mountain pass on State Highway 120 in California’s Sierra Nevada mountain range and one of the entrances to Yosemite NP. The pass itself peaks at 9945 ft above sea level. Each winter it gets a ton of snow, but also with a great deal of variability, which really affects when it can be plowed and the road reopened.
Our family likes to go to Yosemite in June after the kids school lets out and sometimes Hwy 120 and Tioga Pass can often be closed at this time, which limits which areas of the park you can visit. So I often look at data on when the road has opened before and thought it would be a good thing to visualize.
You can toggle the labels on the graph that show the dates of opening and closing as well as the number of days that the pass was closed each winter. Hovering (or clicking) on the circles on the graph will give you a pop up which gives you the exact date.
Data and Tools
The data comes from the US National Park Service for most recent data as well as Mono Basin Clearinghouse for earlier data going back to 1933. Data was organized and compiled in MS Excel. Visualization was done in javascript and specifically the plotly visualization library.

Wordle Stats – How Hard is Today’s Wordle?

Update: Just added the ability to look at some previous puzzles (since I started downloading the data from the Wordlebot). Also, you can now view the answers of the puzzles if you click on the eye icon.
What is the distribution of guesses for the daily Wordle?
Wordle is a game of highs and lows. Sometimes your guesses are lucky and you can solve the puzzle easily and sometimes you barely get it in 6 guesses. When the latter happens, sometimes you want validation that that day’s puzzle was hard. This data viz lets you see how other NY Times Wordle players did against the day’s puzzle.
The graph shows the distribution of guesses needed to solve today’s Wordle puzzle, rounded to the nearest whole percent. It also colors the most common number of guesses to solve the puzzle in green and calculates the average number of guesses. “NS” stands for Not Solved.
Even over 1 year later, I still enjoy playing Wordle. I even made a few Wordle games myself – Wordguessr – Tridle – Scrabwordle. I’ve been enjoying the Wordlebot which does a daily analysis of your game. I especially enjoy how it indicates how “lucky” your guesses were and how they eliminated possible answers until you arrive at the puzzle solution. One thing it also provides is data on the frequency of guesses that are made which provides information on the number of guesses it took to solve each puzzle.
I play in the mornings so the graph data will be updated every day at 7am Pacific Time.
Data and Tools
The data comes from playing NY Times Wordle game and using their Wordlebot. Python is used to extract the data and wrangle the data into a clean format. Visualization was done in javascript and specifically the plotly visualization library.

Colorado River Reservoir Levels

How much water is in the main Colorado River reservoirs?
Check out my California Reservoir Levels Dashboard
I based this graph off of my California Reservoir marimekko graph, because many folks were interested in seeing a similar figure for the Colorado river reservoirs.
This is a marimekko (or mekko) graph which may take some time to understand if you aren’t used to seeing them. Each “row” represents one reservoir, with bars showing how much of the reservoir is filled (blue) and unfilled (brown). The height of the “row” indicates how much water the reservoir could hold. Lake Mead is the reservoir with the largest capacity (at almost 29,000 kaf) and so it is the tallest row. The proportion of blue to brown will show how full it is. As with the California version of this graph, there are also lines that represent historical levels, including historical median level for the day of the year (in red) and the 1 year ago level, which is shown as a dark blue line. I also added the “Deadpool” level for the two largest reservoirs. This is the level at which water cannot flow past the dam and is stuck in the reservoir.
Lake Mead and Lake Powell are by far the largest of these reservoirs and also included are several smaller reservoirs (relative to these two) so the bars will be very thin to the point where they are barely a sliver or may not even show up.
Historical Data
Historical data comes from https://www.water-data.com/ and differs for each reservoir.
- Lake Mead – 1941 to 2015
- Lake Powell – 1964 to 2015
- Flaming Gorge – 1972 to 2015
- Lake Mohave – 1952 to 2015
- Lake Navajo – 1969 to 2015
- Blue Mesa – 1969 to 2015
- Lake Havasu – 1939 to 2015
The daily data for each reservoir was captured in this time period and median value for each day of the calendar year was calculated and this is shown as the red line on the graph.
Instructions:
If you are on a computer, you can hover your cursor over a reservoir and the dashboard at the top will provide information about that individual reservoir. If you are on a mobile device you can tap the reservoir to get that same info. It’s not possible to see or really interact with the tiniest slivers. The main goal of this visualization is to provide a quick overview of the status of the main reservoirs along the Colorado River (or that provide water to the Colorado).
Units are in kaf, thousands of acre feet. 1 kaf is the amount of water that would cover 1 acre in one thousand feet of water (or 1000 acres in water in 1 foot of water). It is also the amount of water in a cube that is 352 feet per side (about the length of a football field). Lake Mead is very large and could hold about 35 cubic kilometers of water at full (but not flood) capacity.
Data and Tools
The data on water storage comes from the US Bureau of Reclamation’s Lower Colorado River Water Operations website. Historical reservoir levels comes from the water-data.com website. Python is used to extract the data and wrangle the data in to a clean format, using the Pandas data analysis library. Visualization was done in javascript and specifically the D3.js visualization library.

Recent Comments