Archive for the ‘Math’ Category:
NY Times Digits Archive

Now play all old Engaging Data Digits puzzles plus 120 archived Digits puzzles from the New York Times
You can still play the NYT Digits Game
Missing the NYT Digits game? You can still play (or replay) the old puzzles here.
On August 8th, 2023, the New York Times ended the beta for their Digits math game and the game is no longer playable. The game ran from April 10th to August 8th and there were 120 different daily puzzles during that time.
Twitter user @Digits_Analysis had compiled a list of each of the five daily puzzles during that entire time period (600 puzzles total) and generously provided them to me. Since I already coded up a Digits replacement with daily puzzles, I figured I could adapt that code fairly easily to make a version where you could play old puzzles. The first 120 puzzles are the original NY Times puzzles and subsequent puzzles are the collection of new daily puzzles.
Rules
The rules for Digits are relatively simple just like in the NYT version. Each day’s puzzle has 5 individual puzzles to complete. Every puzzle has a target number and 6 individual starting numbers that you must use in mathematical calculations to try and create the target number. Each of the 6 numbers can only be used once but the answer to a given math calculation becomes a new number to use.
Once you finish one puzzle, you can use the tabs at the top to move to another puzzle.
Scoring
You get up to 3 stars for each puzzle:
3 stars if you match the target
2 stars if your number is within 10 of the target
1 star if your number is within 25 of the target
Other
Auto-Advance – Click on the gear to toggle on and off “auto-advance”. When enabled, the game will cue up the next puzzle if you hit the target.
Chainmode – Click on the gear to toggle on and off “chainmode”. When enabled, it will automatically highlight the answer from the previous calculation to be the first number in the new calculation.
Share – Share your Digits stars on social media using the share button, which will copy your results to your clipboard. It will share a link to the specific puzzle you are on.
# button – clicking the # button lets you see the total number of possible solutions as well as the fewest and most operations that can yield a solution. This can bring an extra element of challenge to the game. See if you can achieve the shortest solution and then try again to achieve the longest solution. Clicking on the buttons reveals one of the solutions that have the fewest and most number of operations.
Tracking your plays – Digits archive will keep track of your stars for all of 120 daily puzzles. Given that there are 120 old Digits puzzles to play, it may take folks many days, weeks or even months to go through these puzzles. One issue is that on the Safari browser on Macs and iOS devices, the data storage used to track your progress through these puzzles may be deleted if you don’t play the game for 7 days. The browser does this for privacy concerns. Just be aware that your data could be deleted by the browser if you are using Safari and don’t play at least once for 7 straight days. This shouldn’t be a problem for other browsers.
Hopefully you’ll find this enjoy playing the old NYTimes Digits math game and find it a fun and interesting way to improve your mathematical thinking. Let me know if you find any bugs or have any suggestions.
Tools
Python code was used to generate the puzzles and the game play and visuals were created in javascript, CSS and HTML. The New York Times Digits puzzle data was obtained from @Digits_Analysis

Digits Game NYT – A Daily Math Puzzle

Press the # symbol to see the solutions.
Please share Digits with your friends, family, colleagues, math teachers, students and anyone else you think might enjoy this math puzzle game
It’s great to hear from all the folks who have taken the time to play Digits and let me know. I’m glad that so many people are enjoying it.
You can still play the NYT Digits Game
Missing the NYT Digits game? You can still play it here.
On August 8th, 2023, the New York Times ended the beta for their Digits math game and the game is no longer playable. About a week prior to that, a friend asked me to create a clone of Digits so he and his daughter could keep playing together. I had never played before but tried it out. Not surprisingly, since I like games, puzzles and math, I found it to be quite fun. I’m always looking out for interesting things to make, so I figured it would be a fun challenge. I’d previously made some variants of the popular Wordle Game: Wordguessr, Tridle and Scrabwordle.
Rules
The rules for Digits are relatively simple just like in the NYT version. Each day you are given 5 puzzles to complete. Every puzzle has a target number and 6 individual starting numbers that you must use in mathematical calculations to try and create the target number. Each of the 6 numbers can only be used once but the answer to a given math calculation becomes a new number to use.
Once you finish one puzzle, you can use the tabs at the top to move to another puzzle.
Scoring
You get up to 3 stars for each puzzle:
3 stars if you match the target
2 stars if your number is within 10 of the target
1 star if your number is within 25 of the target
Other
Auto-Advance – Click on the gear to toggle on and off “auto-advance”. When enabled, the game will cue up the next puzzle if you hit the target.
Chainmode – Click on the gear to toggle on and off “chainmode”. When enabled, it will automatically highlight the answer from the previous calculation to be the first number in the new calculation.
Share – Share your Digits stars on social media using the share button, which will copy your results to your clipboard.
# button – clicking the # button lets you see the total number of possible solutions as well as the fewest and most operations that can yield a solution. This can bring an extra element of challenge to the game. See if you can achieve the shortest solution and then try again to achieve the longest solution. Clicking on the buttons reveals one of the solutions that have the fewest and most number of operations.
Hopefully you’ll find this replacement to the NYTimes Digits math game a fun and interesting game and improve your mathematical thinking. Let me know if you find any bugs or have any suggestions.
Why did the New York Times discontinue Digits?
I’m guessing it wasn’t as popular as some of their other games. Wordle and the crossword puzzle are probably the most popular. And they seem to be pushing their new game Connections as a sort of replacement for Digits. But alot of folks like math games so it’s a bit of a shame that they discontinued it, especially since it’s simple to learn how to play but can be challenging to get the solution each time.
Tools
Python code was used to generate the puzzles and the game play and visuals were created in javascript, CSS and HTML.

Van Gogh As Drawn By A Traveling Salesman

This “art project”, like the Mona Lisa one, draws a portrait of Vincent Van Gogh as a single continuous line. When it’s on the slow setting, is oddly satisfying and calming to watch the picture get drawn.
Click the “Draw Van Gogh” button below to see his famous self portrait drawn with a single continuous line with 120,000 segments.
The traveling salesman problem (TSP) is a classic problem in operations research and mathematical programming. It seeks to answer the question, given a set of destinations, what is the shortest possible travel route someone could take to visit them all. It is a notoriously challenging problem to solve when the number of destinations grows. A picture of the famous Van Gogh self-portrait was converted to 120,000 dots and a challenge was created to find the most optimal solution to visiting each of these 120 thousand points (i.e. drawing the shortest continuous line that goes through each and every point.
The current most-optimal solution that has been found to this Van Gogh self-portrait challenge was calculated in 2013 by Honda, Nagata and Ono. I used the order of destinations (also called the “tour) that he developed and animated the line segments to create an animated drawing of the portrait as a single continuous line.
Here an analogous TSP drawing for the Mona Lisa.
Each time you click on the “Draw Van Gogh” button, it chooses a different starting point but follows the same order of destination points, looping around until all the points are visited.
You can also change the speed at which the individual line segments are drawn. It is surprisingly relaxing and satisfying to watch the line wind its way around the screen to fill in the famous Van Gogh self-portrait.
For a very high res version of the entire photo click here (around 4 MB file size).
Data and Tools:
I downloaded the 120,000 points and the tour from Honda, Nagata and Ono that is currently the shortest that has so far been calculated from the TSP Art website and the University of Waterloo.
Javascript was used to draw on the HTML canvas and animate the process.

Visualizing the outcome of Eeny Meeny Miney Moe
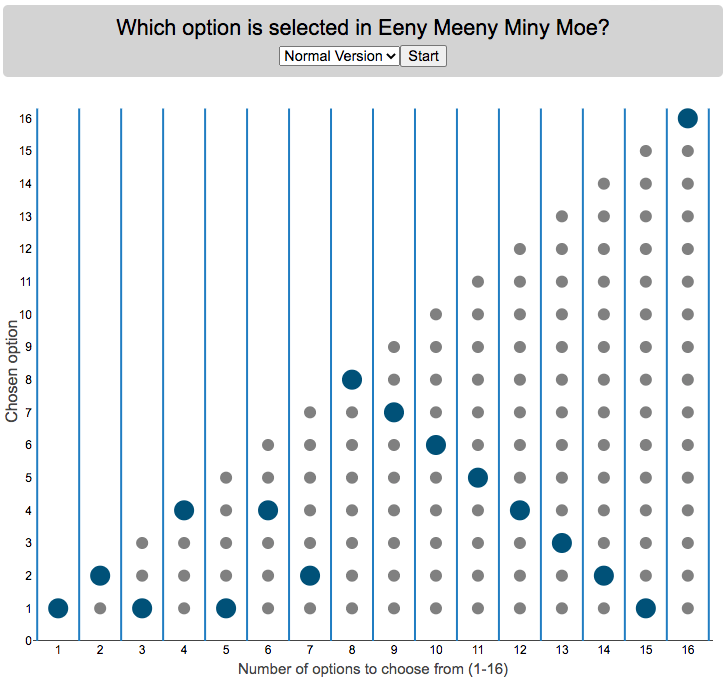
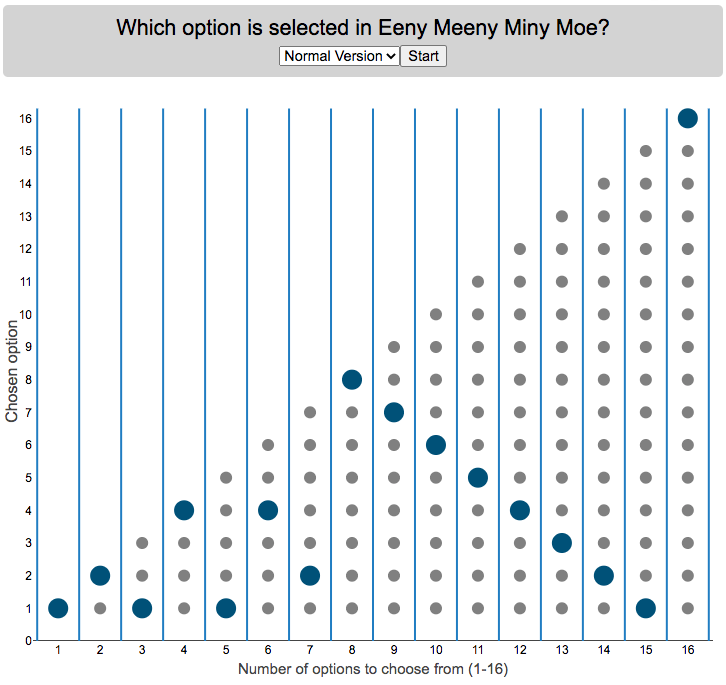
Who is selected when kids do Eeny Meeny Miney Moe?
I was watching my kids try to pick who got go first by doing the kids rhyme,
“Eeny, meeny, miny, moe, catch a tiger by the toe, if he hollers let him go, eeny, meeny, miny moe.”
Since there were only two of them, it got me thinking, if you knew which one it would fall on at the end, you could decide who to start counting with to ensure that you select who you want. For each set with different numbers of options, you will get a different individual from that set chosen so I thought I’d visualize who gets selected.
Click “Start” to see which option gets selected when there are different numbers of options. Hover over the graph to see which option is chosen.
There are multiple variants of the rhyme, but the primary one mentioned above has 16 counting elements. The math is such that you take the modulo (which is equivalent to a remainder in long division). For example, if you have 15 choices for the 16 element phrase, you’ll count through all 15 and then go back to the first option and end on it (i.e. item number 1 is chosen). 16 divided by 15 has a remainder of 1. In the case that the remainder is zero, you choose the last item. I.e. if there are 16 items/people to choose among, the last option is chosen and the remainder will be 0.
Longer variants will have more words, which are also shown on the dropdown menu. If you know of other variations, let me know in the comments and I can add them.
Primary: “Eeny, meeny, miny, moe, catch a tiger by the toe, if he hollers let him go, eeny, meeny, miny moe.” – 16 counting elements (“catch a” is one element, “by the” is another, etc)
Variation#1: “Eeny, meeny, miny, moe, catch a tiger by the toe, if he hollers let him go, eeny, meeny, miny moe My mother told me to pick the very best one and that is Y O U” – 31 counting elements
Variation#2: “Eeny, meeny, miny, moe, catch a tiger by the toe, if he hollers let him go, eeny, meeny, miny moe My mother told me to pick the very best one and you are it” – 29 counting elements
Source and Tools:
The rhymes come from my childhood and my kids helped me remember some of the variants. Calculations are done in javascript and visualization is done with the open source Plotly javascript graphing library.
The Mona Lisa As Drawn By A Traveling Salesman

The traveling salesman problem (TSP) is a classic problem in operations research and mathematical programming. It seeks to answer the question, given a set of destinations, what is the shortest possible travel route someone could take to visit them all. It is a notoriously challenging problem to solve when the number of destinations grows. A picture of the famous Mona Lisa was converted to 100,000 dots and a challenge was created to find the most optimal solution to visiting each of these 100 thousand points (i.e. drawing the shortest continuous line that goes through each and every point.
The current most-optimal solution that has been found to this Mona Lisa challenge was calculated in 2009 by Yuichi Nagata. This art is created using the order of destinations (also called the “tour) that he developed.
Click the “Draw Mona Lisa” button below to see the famous painting drawn with a single continuous line with 100,000 segments.
Each time you click on the “Draw Mona Lisa” button, it chooses a different starting point but follows the same order of destination points, looping around until all the points are visited.
You can also change the speed at which the individual line segments are drawn. It is surprisingly relaxing and satisfying to watch the line wind its way around the screen to fill in the famous picture of the Mona Lisa.
For a very high res version of the entire photo click here (around 4 MB file size).
Data and Tools:
I downloaded the 100,000 points and optimal tour from Yuichi Nagata from the TSP Art website and the University of Waterloo.
Javascript was used to draw on the HTML canvas and animate the process.

Estimating pi (π) using Monte Carlo Simulation
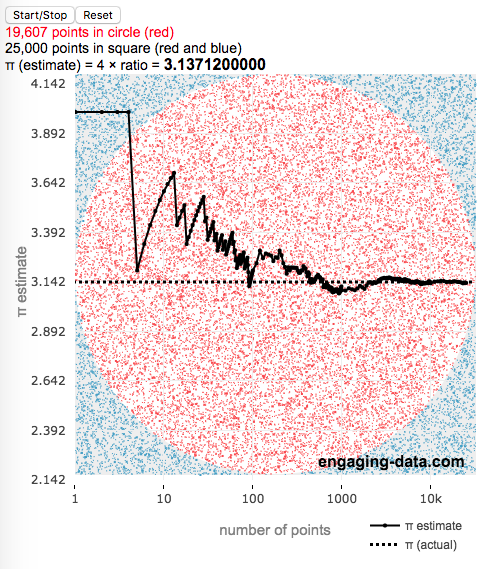
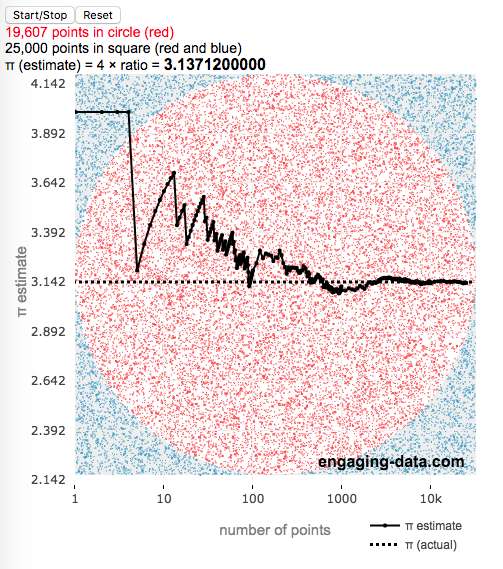
This interactive simulation estimates the value of the fundamental constant, pi (π), by drawing lots of random points to estimate the relative areas of a square and an inscribed circle.
Pi, (π), is used in a number of math equations related to circles, including calculating the area, circumference, etc. and is widely used in geometry, trigonometry and physics.
This app estimates the value of pi by comparing the area of a square and an inscribed circle. The areas are calculated by randomly placing dots into the square and then counting how many of them are also inside the circle. If you do this enough times, you will get a rough ratio of the relative areas of the two shapes. These points are plotted on the graph (red if the fall inside the circle and blue if the fall outside).
Also shown on the graph is the value of our estimate of pi as the simulation progresses, from a few points to many thousands, to millions of points. We can see that when we have only a few points, the value may not be very accurate but as the number of points increases the value of our estimate gets closer to the true value. Running the simulation will add and plot 1 million points. After the first 100 points are added, the rate at which points are added increases. You’ll notice this as the speed at which dots fills up the square increases and because the plot is shown with a logarithmic x-axis.
Here is the math:
Length of side of square: $2 \times r$
radius of circle: $r$
Area of square: $A_{square} = 4r^2$
Area of circle: $A_{circle} = \pi r^2$
The ratio of areas is $A_{circle}/A_{square} = \pi r^2 / 4r^2 = \pi / 4$
Solving for pi: $\pi = 4 \times A_{circle}/A_{square} \approx 4 \times N_{dots_{circle}}/N_{dots_{square}}$
So pi is estimated as 4 times the ratio of dots in the circle vs square
Tools:
This was programmed in javascript, canvas and plotted using the open source plotly javascript plotting library.
Recent Comments