Posts for Tag: mountains
What are the highest mountains on Earth? Measuring from sea level vs center of earth
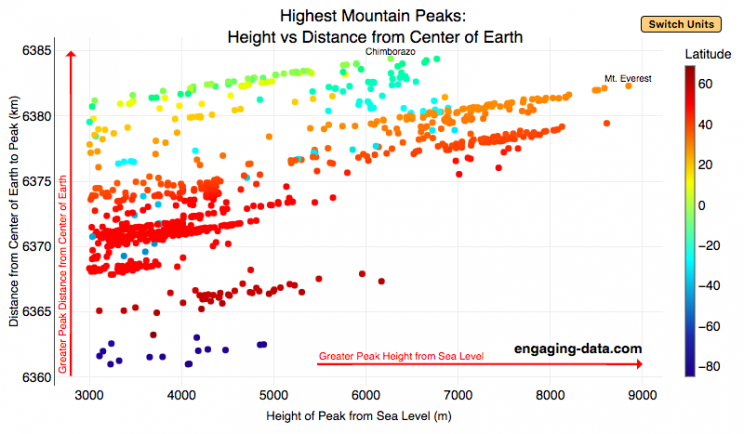
The Highest Mountains On Earth Depend On How You Measure “High”
Mount Everest is famous for being the highest mountain on Earth. The peak is an incredible 8,848 meters (29,029 ft) above sea level. But that is only one way to measure the height of a mountain. Chimborazo, a mountain in Ecuador, holds the distinction for the mountain whose peak is the furthest from the center of the Earth. How is that possible? This is because the Earth is not a perfect sphere. Rather, due to the spinning of the Earth around it’s axis, the centrifugal force causes the equator to bulge out slightly. This flattened shape is called an oblate spheroid and makes the radius of the earth at the equator about 22 km (about 0.3%) larger than the radius to the poles. Mountains close to the equator will “start” further away from the center of the earth, than those at higher latitudes.
This graph plots over 800 of the highest mountains on Earth with their peak height above sea level on the x-axis and their peak distance from the center of the earth on the y-axis. Each point represents one mountain. The colors of the plots correspond to the latitude of the mountain. These mountains range from 3000 meters in height to 9000 meters in height. You can hover over a data point (or click on mobile) to get more information about the mountain. You can also switch from metric to imperial units with the button on the graph.
For a given mountain range at a certain latitude, you can see that as the mountain heights above sea level increases, so does their distance from the center of the Earth. Mountains in the southern hemisphere are colored in blue, those around the equator are green and yellow, and those in the northern hemisphere are red and orange. The mountains with the highest peaks above sea level are shown on the right side of the graph in red and orange (mostly in the Himalaya), with Mt Everest as the right most point on the graph (nearly 9000 meters tall).
Mountains with peaks the greatest distance from the center of the earth are found near the equator in light green/yellow and are found at the top of the graph. You’ll notice that a number of these mountains are higher than Mt Everest when looking at the distance from the center of the earth.
The Himalayas are the “highest” mountains on earth if you are measuring height from sea level, while the Andes are the “highest” if you measure from the center of the earth.
Calculating Distance from Earth’s Center to Mountain Peak
The distance from the center of the Earth is calculated from the following formula:
$$D_{mountain} = H_{mountain} + R_{lat}$$
where $D_{mountain}$ is the distance from center of earth to the top of the mountain, $H_{mountain}$ is the mountain height above sea-level and $R_{lat}$ is the radius of earth at the mountain’s latitude. The height is data that was downloaded from a list of mountain heights.
and the radius of the earth for a given latitude is calculated using the formula:
$$R_{lat}=\sqrt{a^2cos(lat)^2+b^2sin(lat)^2\over acos(lat)^2+bsin(lat)^2)}$$
where $a$ and $b$ are the equatorial and polar radii (6378.137 km and 6356.752 km respectively).
Earth Radius Calculator
Here is a calculator for determining the radius of Earth at a given latitude:
You can use this to calculate the distance from the center of the earth to sea level at your latitude.
Data and Tools:
Data on the heights of over 800 mountain peaks over 3000 meters in height was downloaded from Wikipedia. There ended up being alot of google searching and data cleaning to get it into suitable format for plotting. The calculations were made with javascript and plotted using plotly, the open source javascript graphing library.
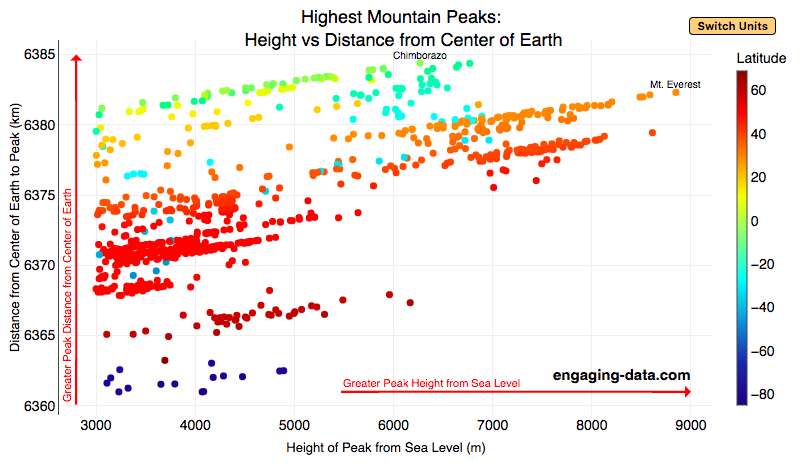
What are the highest mountains on Earth? Measuring from sea level vs center of earth

The Highest Mountains On Earth Depend On How You Measure “High”
Mount Everest is famous for being the highest mountain on Earth. The peak is an incredible 8,848 meters (29,029 ft) above sea level. But that is only one way to measure the height of a mountain. Chimborazo, a mountain in Ecuador, holds the distinction for the mountain whose peak is the furthest from the center of the Earth. How is that possible? This is because the Earth is not a perfect sphere. Rather, due to the spinning of the Earth around it’s axis, the centrifugal force causes the equator to bulge out slightly. This flattened shape is called an oblate spheroid and makes the radius of the earth at the equator about 22 km (about 0.3%) larger than the radius to the poles. Mountains close to the equator will “start” further away from the center of the earth, than those at higher latitudes.
This graph plots over 800 of the highest mountains on Earth with their peak height above sea level on the x-axis and their peak distance from the center of the earth on the y-axis. Each point represents one mountain. The colors of the plots correspond to the latitude of the mountain. These mountains range from 3000 meters in height to 9000 meters in height. You can hover over a data point (or click on mobile) to get more information about the mountain. You can also switch from metric to imperial units with the button on the graph.
For a given mountain range at a certain latitude, you can see that as the mountain heights above sea level increases, so does their distance from the center of the Earth. Mountains in the southern hemisphere are colored in blue, those around the equator are green and yellow, and those in the northern hemisphere are red and orange. The mountains with the highest peaks above sea level are shown on the right side of the graph in red and orange (mostly in the Himalaya), with Mt Everest as the right most point on the graph (nearly 9000 meters tall).
Mountains with peaks the greatest distance from the center of the earth are found near the equator in light green/yellow and are found at the top of the graph. You’ll notice that a number of these mountains are higher than Mt Everest when looking at the distance from the center of the earth.
The Himalayas are the “highest” mountains on earth if you are measuring height from sea level, while the Andes are the “highest” if you measure from the center of the earth.
Calculating Distance from Earth’s Center to Mountain Peak
The distance from the center of the Earth is calculated from the following formula:
$$D_{mountain} = H_{mountain} + R_{lat}$$
where $D_{mountain}$ is the distance from center of earth to the top of the mountain, $H_{mountain}$ is the mountain height above sea-level and $R_{lat}$ is the radius of earth at the mountain’s latitude. The height is data that was downloaded from a list of mountain heights.
and the radius of the earth for a given latitude is calculated using the formula:
$$R_{lat}=\sqrt{a^2cos(lat)^2+b^2sin(lat)^2\over acos(lat)^2+bsin(lat)^2)}$$
where $a$ and $b$ are the equatorial and polar radii (6378.137 km and 6356.752 km respectively).
Earth Radius Calculator
Here is a calculator for determining the radius of Earth at a given latitude:
You can use this to calculate the distance from the center of the earth to sea level at your latitude.
Data and Tools:
Data on the heights of over 800 mountain peaks over 3000 meters in height was downloaded from Wikipedia. There ended up being alot of google searching and data cleaning to get it into suitable format for plotting. The calculations were made with javascript and plotted using plotly, the open source javascript graphing library.

Recent Comments